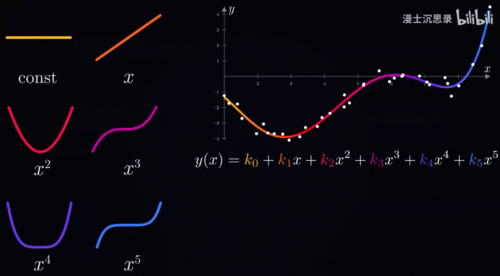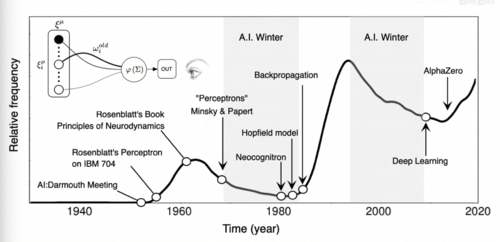
1956年一群科学家齐聚达特茅斯开了一场会，这场会议持续一个多月，一共只有十来个人参加，但个个都是大佬

他们包括达特茅斯的数学系教授麦卡锡，哈佛大学数学与神经科学研究员闵斯基，IBM主管罗切斯特，信息论发明人香农等人，但就是这样一场很小的会议深刻的改变了几十年后世界的样貌。8年前战胜李世石的AlphaGo，如今能帮我们解决各种日常问题的GPT，本质上都起源于这场会议所发起的研究，如何制造出一种可以不断学习

并模拟人类智能的机器，这个领域在2018年拿到图灵奖之后，又在今年一举斩获了诺贝尔物理奖和化学奖，这个领域就叫人工智能。而这场会议也被视为开创人工智能的起点-达特茅斯会议。

人工智能说白了就是人工搭建起一套智能，要实现这个目标，首先就要回答一个非常根本的问题什么是智能

，尽管有关智能的定义千千万，但他们都逃不开这样的核心，智能本质上就是通过收集信息，对于不同的情景作出针对性的反应。既然智能说白了就是看情况做事，那么所谓人工智能，同样就是搭建起一个根据不同的环境信息

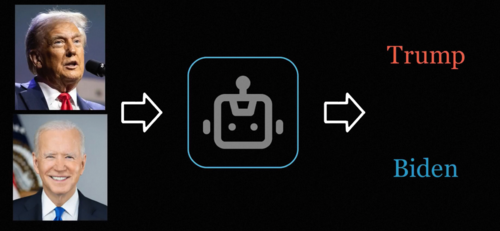
给出针对性的输出和回应的系统，这个输出可以是动作语言也可以是一种判断和预测，比如说人脸识别可以根据不同的人脸针对性地反馈出不同人的身份信息。GPT可以根据上文不同的问题和任务的要求，针对性的跟你说话并解决问题，因此它们都是智能。

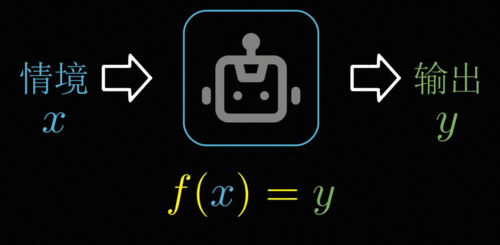
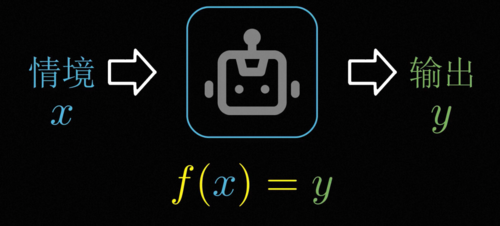
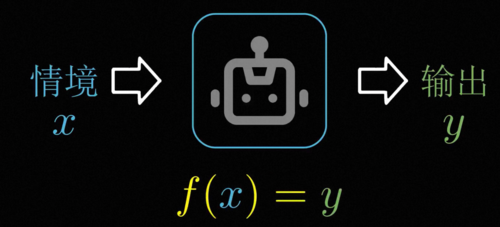
总而言之，智能的本质就是一个不会乱来的黑箱，或者用数学一点的说法，智能就是找到情景信息的输入和我们想要的聪明的行为输出之间的函数对应关系。

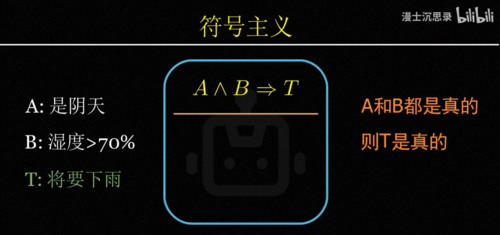
该怎么做出这样一个聪明的黑箱呢，科学家针对这个问题提出了很多思路，例如有一批人从数学的形式化推理体系中得到灵感，主张智能可以用符号的逻辑推理来模拟，这就是符号主义symbolism。

举个例子，a表示阴天，b表示湿度大于70%，t表示将要下雨，那么知识是一条逻辑规则，如果a和b是真的，那么t就是真的。所谓智能，就是看到阴天和湿度很大，明白a和b都对，那么利用这条规则推出t是真的，从而预测到可能将要下雨，这些人类的推理和思考都可以从这些符号和规则当中，像算数一样计算出来，因此符号主义相信智能正是一套像这样处理符号和规则的计算系统，他把人类的知识和逻辑用如果a，那么b这样的规则存储下来，然后不断进行符号推演，就可以实现接近人类的智能，这套思路最成功的典范，就是曾经的专家系统。

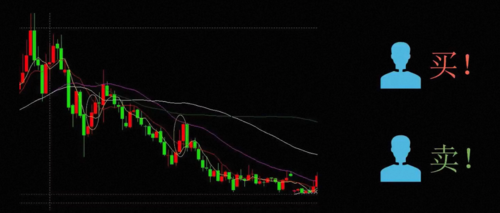
这套系统一度在疾病诊断和金融咨询领域获得了很大的成功，但随着时间推移，它也逐渐暴露出致命的缺陷。首先很多时候现实世界没有那么清晰的规则，即使询问人类专家出现某个症状是不是得了某个病，或者股票走势涨成这个样子，应该是买还是卖，他们给出的回答往往都并不一致，那你的系统只能选择一个，到底该听谁的呢。

更要命的是这套系统完全是在复制人类经验，所以他的能力上限就是专家的水平，无法做到比人更好，而且从你设计完成这套系统开始，他就永远是静止不变的水平，很难像人一样随着经验和时间的增长水平不断继续提升。

正因此从上世纪70年代开始，另一个人工智能流派开始发扬光大，他不追求一开始就有一个完美的黑箱，但允许这个黑箱不断的变化，通过不断的引导和学习，让他在某一个任务上表现的越来越好，也是一种成长型的心态。

这种思路就像训狗，你发出坐的指令，如果它坐下来，你就奖励它狗粮或者摸摸狗头，如果它没听懂或者瞪着个眼睛，你就给它一逼斗。久而久之，一只会听指令的聪明小狗就训练完成了，这个流派的名字也很生动，就叫做机器学习。

顾名思义通过给机器以奖励或者惩罚的方式，让机器自主调整不断学习，从而学会解决某一种任务的智能，这个任务可能是识别图片里的数字和人脸，也可能是下围棋或者是与人对话等等，机器学习的强大之处在于它不需要任何专家的专业知识来人为搭建黑箱内部的结构，它只需要两样东西，一个强大且有学习能力的黑箱，以及足够多的数据。

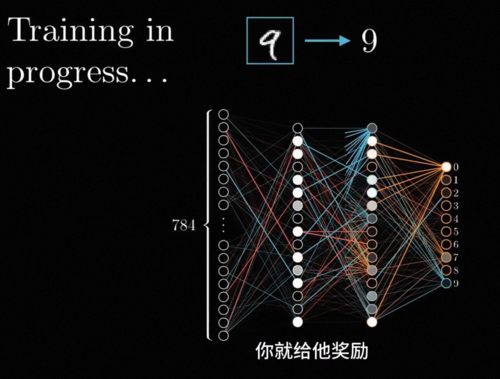
举个例子，假设你想要一个能够识别数字的智能黑箱，那么只需要准备一个具有学习能力的机器，然后收集很多数字的图片，人工标注出每张图片里的数字是什么，接下来你只需要像训狗一样，把一张张图片展示在这个机器面前，让他预测里面的数字到底是什么，如果他预测对了你就给他奖励，错了你就给他惩罚，让这个机器不断的自我调整，当他见过的图片越来越多之后就能够神奇的做到正确识别这个图片里的数字是什么了。

哪来这种神奇黑箱？那怎么奖励一个机器？机器怎么建立条件反射？

这三个问题其实就分别对应于机器学习的模型、结构损失函数和训练过程。

怎么搭建起一个有学习能力的黑箱机器？

有没有一种万能的超级强大的黑盒，无论什么样的对应关系，它都能表示和学会呢，这里就值得一提另一派实现人工智能流派-联结主义，他们认为大自然已经给出了实现智能的标准答案，那就是人类精妙的大脑，只需要通过仿生的方式模拟单个神经元的复杂功能，以及神经元之间复杂的连接，那么我们只需要像运行一台精密的钟表一样，运行这个人工搭建的神经网络，人类就可以实现不可思议的智慧，这一派被称作联结主义connectionism。

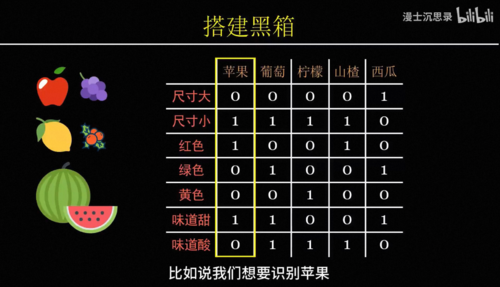
为了理解连接主义，我们先考虑一些最简单的智能，比如这里有一个苹果，为什么你会觉得它是一个苹果呢。你可能会说因为它直径大约10厘米，外表皮是红色的，是个球形，气味香甜。没错，我们对于很多概念，比如苹果的理解是依赖于其他概念属性组合而来的，在每个不同的概念属性上不同的水果会有各自的特征。

在计算机的世界里，我们用1来表示符合，0表示不符合，这样我们就可以列出各种水果，与不同属性之间的一张关系对应表，当每个水果的特征都和苹果的属性吻合时，我们就倾向于判断这是苹果，如此我们就拥有了一种简单的

识别水果的智能。

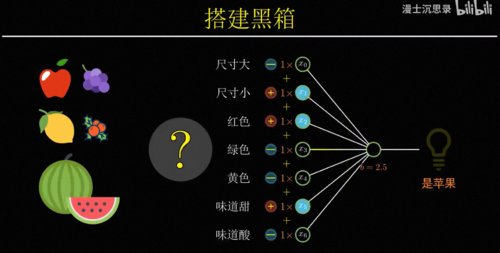
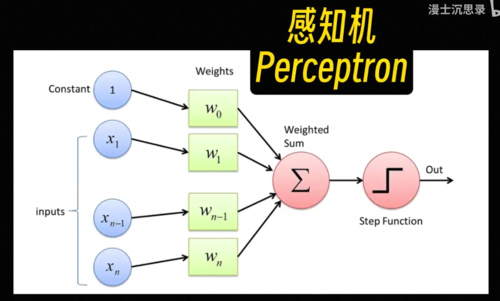
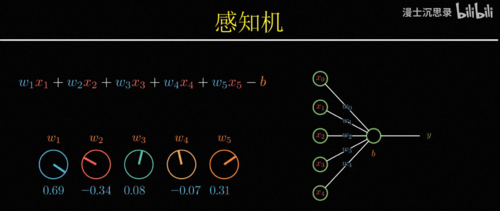
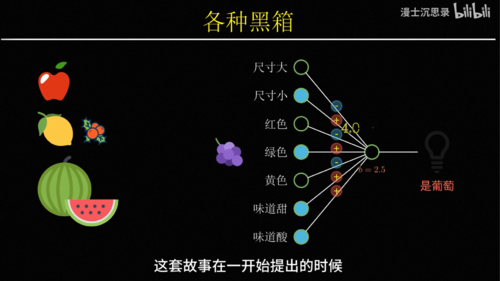
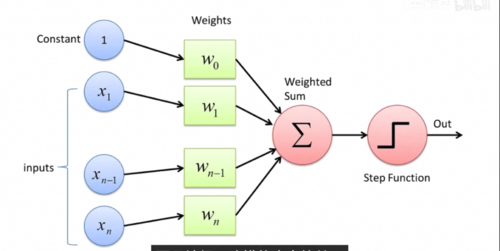
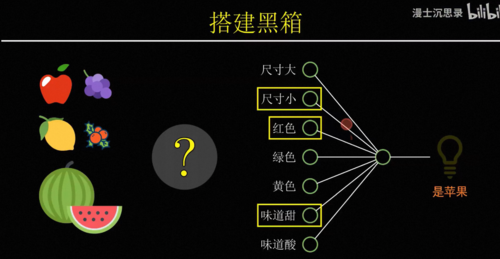
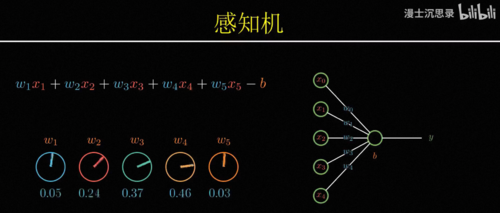
因此有一种最简单的搭建黑盒的方式，比如说我们想要识别苹果，就将一个水果的所有特征，比如说大小、颜色、气味什么的作为输入，然后分别考虑它的每个特征是否像一个苹果，具体来说就是乘一个系数，比如说尺寸不大、颜色是红色、味道很甜，这些都表明这个水果符合苹果的特征，因此他们对于是苹果这个判断起到正向的促进作用，我们会把它乘以一个正数，而尺寸很大吃起来酸，这些特征都表明不太可能是苹果，所以我们把它乘以负的系数，最后我们只需要将这些特征，各自乘以它们对应的系数，然后加在一起就可以得到一个苹果得分，这个得分越高越像苹果，越低则越不像，所以我们就可以再设置一个得分的预值b，如果最后的得分高于b，那么这台机器就激活，否则不激活。

此时整个这台机器就变成了一个苹果识别机，只有你把苹果拿到它面前的时候，它会激活亮起右边的灯泡，而只要你放在前面的水果不满足苹果的特征，它就不会激活，所以根据我们的定义整个黑箱，此时就具备了识别苹果的智能，这个黑箱机器的厉害之处在于你不仅可以用它来识别苹果，还可以用来识别其他的水果，只需要通过调整这些连接的系数，你就可以表示不同的概念，比如说你可以让他在水果又大又绿又甜的时候激活，那么此时这台机器的用途就是识别出西瓜，或者在又小又红又酸的时候激活，那么他就可以特别的筛选出山楂，这里每一个特征到输出之间连接的系数就像一个机器的旋钮，你只需要根据自己的需要设置这些旋钮的值，就可以让整台机器非常针对性的只对某种水果激活，而这种从输入数据中识别不同水果特征的模式，理解概念的过程就叫做模式识别。

这个玩意儿就是人类在1956年最早提出的一种模式识别的算法模型：感知机。

有人可能会说了你这个取各种条件合在一起判断的过程，看起来和前面的专家系统好像也没啥区别呀。你说的很对，这是一个很多人都不知道的冷知识，大家通常以为神经网络代表的联结主义，从一开始就和符号主义水火不容

分道扬镳，但其实感知机这种最早期的神经网络，它的设计很大程度上借鉴甚至是脱胎于逻辑推理，其思路同样是组合不同的特征条件来进行推理，这里的每一个神经元，也就像刚才我们说的符号逻辑当中的一个一个命题的字母一样，只不过他是用数值计算的方式来模拟逻辑的，而数值计算本身不局限于有限且明确的符号推理，因而在更广泛的领域，比如说控制环境感知图像识别等领域具有更强大的潜力。

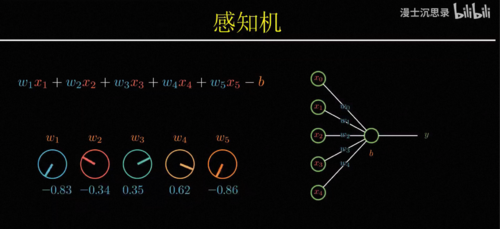
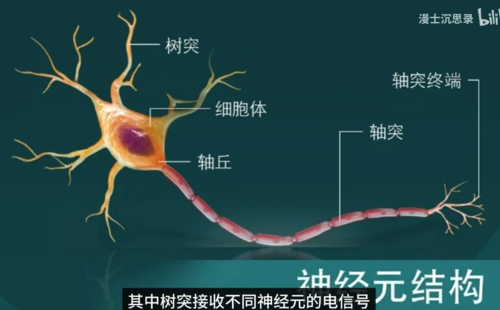
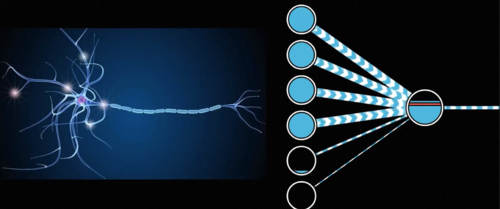
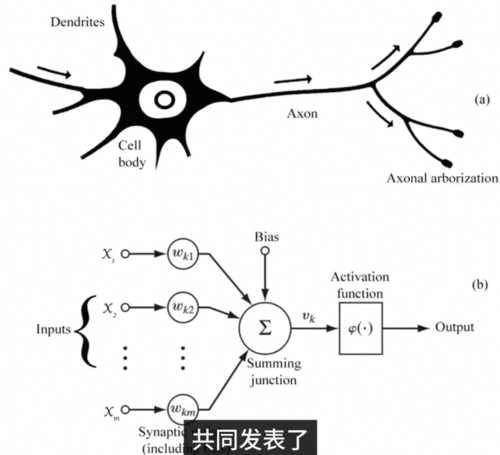
巧合的是这种设计同样和神经科学不谋而合，中学的时候我们学过神经元通过电信号传递信息，其中树突接收不同神经元的电信号，而轴突则会将自己的信号传递给其他的神经元，而感知机也恰似一个神经元，你看那些传入的数字分别表示它接收到的各种信号，它们可能会激活或者抑制这个神经元的活动，而这种影响就体现在每条连边参数w的正负和大小上，神经元直接叠加所有接收的影响，而如果叠加的刺激足够大，它就会激活进一步往后传递，这一切都和生物神经元的活动不谋而合。

事实上这个数学模型的提出比人工智能还早，早在1943年的二战期间Pitts和Mcculloch在生物物理学通报上共同发表了神经活动中内在思想的逻辑演算，提出了这套神经元的数学模型。

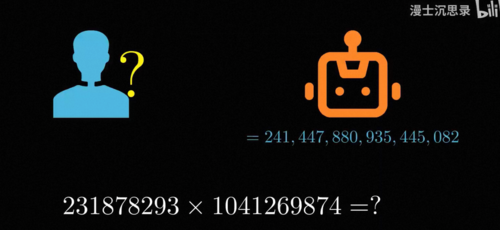
你注意看这套名字-神经活动中内在的逻辑验算，这更加表明联结主义和符号主义其实是同源的。1957年康奈尔大学的罗森布拉特造出了人类第一台有实际应用价值的：感知机。这台感知机将图片的像素作为输入，通过算法调整参数不断学习，最终能够做到判断出一张图片里是男人还是女人或者是左箭头还是右箭头，一时间轰动世界，虽然在今天看来这可能没什么，但让我换一个角度跟你解释，你就会知道这有多了不起，计算机和人是两种非常不同的东西，对于人来说很困难的问题，比如说计算两个十位数的乘法，对于计算机来说却很简单。

但对人来说很简单的事情，对于计算机来说却非常困难，比如说理解图片的内容。

因为在计算机看来图片本质上是一堆像素的数值，所以识别图片中的内容，在数学本质上就是给你一大坨数字组成的矩阵，然后问你这里面画的到底是一个什么，或者问你这里面到底是个男人还是女人，人的长相千姿百态，各种五官光影角度的细微变化都会呈现出不同的图片，导致像素的具体数值出现剧烈的变化，而我们要通过纯粹的计算算出来真实照片里的人是男性还是女性，现在你还觉得这整个数学问题，也就是说从图片中看出是什么内容很容易吗，人类的视觉和大脑是不是很不可思议呢，而这个领域就叫做计算机视觉。

正因此在发明感知机之后，时年30岁的罗森布拉特意气风发，迫不及待的召开新闻发布会，畅谈自己研究成果的美好未来，吸引了众多媒体的极大关注。比如说大名鼎鼎的纽约时报记者对感知机的先进性赞不绝口，报道说这是一个能够行走拥有视觉能够写作，能自我复制，且有自我意识的电子计算机的雏形，他把它称为电子大脑，电脑这个名字最早也是从这个时候来的，文章当时还非常乐观的估计，再花上10万美元，一年之后上述构想就可以实现，那时感知机将能够识别出人并能叫出它们的名字，而且还能把人们演讲的内容及时的翻译成另一种语言记录下来，但经历过现实的我们知道，这件事直到最近几年才算真正实现，所以真心也好，忽悠投资人也罢，总之人类对于自己不了解的东西就是很容易浪漫，也很容易对于未来过分乐观，历史上每当人工智能取得一点点微小的进步，人类就会开始赋予它无限能力的想象，畅想与AI大战的场景，从来如此。

回到一开始的问题，那究竟该怎么搭建出一个有学习和进化能力的聪明黑盒子呢，感知机就是一个简单的例子，专业的说法都叫模型，模型本身确定了它输出的函数形式，比如说这里就是先用w i加权组合所有的输入，然后减去预知b，再激活就是它整个模型的输出，这有一套函数形式，但与此同时，它又没有完全确定整个函数，依然有一系列

你需要调节和设定的数值，比如说这里的每个w i和b，它们叫做参数。

我们只需要在设计模型的时候让它足够强大，任何你想要它实现的功能，本质上都可以通过设定模套参数实现，那么我们只需要让这个模型不断调整自己的参数不断向着越来越有用，符合我们需要的这种输出的模式变化，就可以让他最终实现强大的智能，这就是联结主义的信念。

这套故事在一开始提出的时候，野心勃勃，而且实现了感知机这样了不起的成就，但联结主义一度陷入寒冬，甚至被整个世界斥为骗子，在最一开始的时候，就有很多学者反对联接主义，他们觉得这只是机械的模拟了生物的构造，而且神经元建模的也太简单了，他们还觉得联接主义期待在一通乱联当中发生魔法。

1969年马文闽斯基写了一本叫做感知机的书，正如给你伸大拇指的人不一定是夸你也可能是想拿炮打你。

他这本书可不是要推广感知机，而是要给感知机下死刑，把棺材板上的钉子钉死。

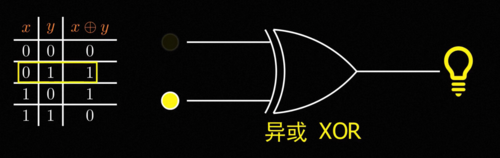
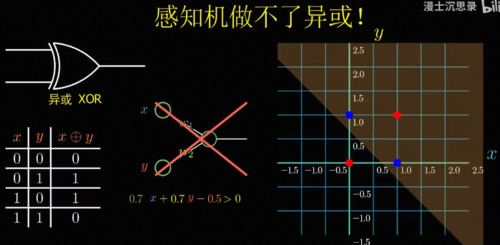
闽斯基在书中指出了这样一个事实，有一个逻辑电路里非常基本的操作叫做异或XOR。

简单来说就是当输入的两个特征一样的时候输出是0，而输入的不一样的时候输出是1，就是这么一个非常简单的对应关系，感知机却无法完成，为什么会这样呢。

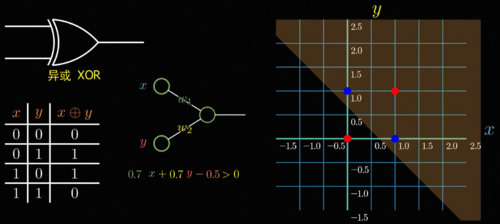
我们仔细看感知机的函数形式就会发现，它本质上是在计算w1x加w2y减b的符号，假如我们把所有的这样的x,y输入画在二维平面的坐标系上，那么能够让感知机激活的所有输入满足w1x加w2y减b大于0，中学的小伙伴可能会很熟悉，这其实就是一个线性规划。

所以说能够激活的满足条件的输入和不激活的分界线永远是一条直线，然而对于异或问题，你会发现需要激活的这两个点和不激活的这两个点是这样分布的，你永远没法用一条直线将这两种点恰好分在直线的两边，所以就不存在一台感知机能够直接实现这个简单的异或运算，闽斯基在这本书里直接毫不客气地说罗森布拉特的论文没有什么科学价值，他本人在同年获得图灵奖，这本书也因此将整个连接主义打入冷宫，在之后的二三十年间神经网络这个名字仿佛就是骗子的代名词，是连异或这个操作都做不好的无用的玩物，在当时图灵奖得主的带头唱衰下，神经网络一度陷入了极度的寒冬，所有人都认为他是垃圾和骗子，基金资助大为减少，研究者纷纷转行，AI研究也因此陷入长达几十年的寒冬。

你看人类又是这么容易悲观，一个小小的反例就自暴自弃，放弃了充满潜力的研究方向，但与此同时

依然有一批研究者在坚持，他们最后守得云开见月明，成为了后来深度学习的奠基人并获得图灵奖，我们可以听听图灵奖和诺贝尔奖双料得主辛顿当年在UCD大学接受采访的时候的一段表达。

主持人：回望你的整个学术生涯，你对其中的哪个方面最为自豪？我并不仅仅在说您的科学发现，而包括您更大的整个生涯，那些与你合作的人，你建立的团队。

辛顿：我想我最骄傲的事我当年坚持了神经网络，尽管当时人们都说这是垃圾，而且说了整整40年。在智力上的学术成就，我最自豪的事玻尔兹曼机，它是反向传播之外的另一种可能。

他们是怎么拯救神经网络的呢，回到刚才异或的的例子，他们想既然一个神经元不行，那么多来几个可不可以呢。

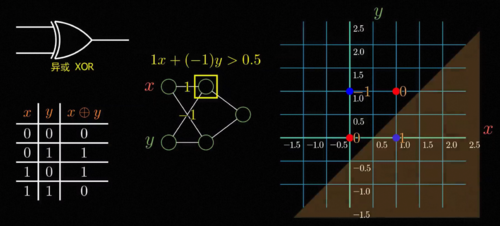
比如说我们将这些感知机的输出一个一个的拿出来，然后在后面再嵌套接一层感知机，作为他们下一个感知机的输入我们一套娃，套娃一层又一层出来一个新的感知机，这样我们就可以让中间一层的两个神经元分别只被0,1和1,0激活，比如说第一个神经元它的组合系数是1，-1，此时就只有1，0这个输入能给它最强的刺激大小为1，其他的都不超过0，所以我们如果再设置一个1/2的阈值就可以让它只在1，0这个输入的时候激活。同理我们也可以对另一个神经元在0,1的情况下才会激活，设置方式是系数-1，1。这样的话，两个中间的神经元就可以分别关注两个我们想要激活的位置，接着我们再把这两个神经元的输出直接加在一起，大于0的时候给出最终的激活，这样整个模型

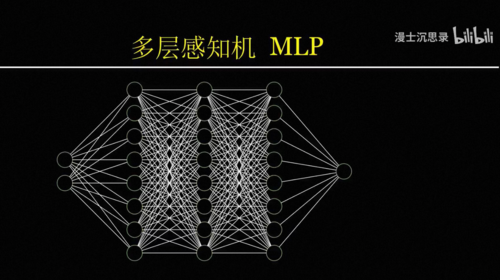
就可以刚好在1，0和0,1的时候激活，而在0，0和1，1的时候不激活，从而实现异或功能，而这就是后来大名鼎鼎的MLP Multilayer Perceptron，全名多层感知机。

这里中间层当然可以不止两个神经元，层数也可以不止两层，当这些神经元层层叠叠的时候，就是大名鼎鼎的神经网络。这里的每一根连线都标志着两个神经元之间的连接强度，是一个可以调节的参数系数。

计算机科学家证明只要这个神经网络的深度和宽度都足够大，那么理论上它可以拟合任何一种函数，表达任何一种智能所需要的，输入到输出之间的对应关系，换言之，只要你有一个超大的神经网络，那么任何一个你想要的智能黑箱的功能都一定可以通过设定一套参数实现。

该怎么理解神经网络这种强大的能力呢，还记得我们前面说过我们用不同的属性概念组合再激活就得到了一个

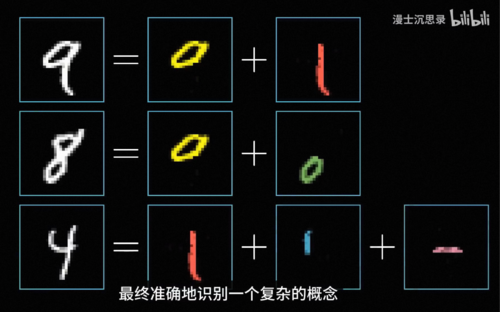
可以识别苹果的感知机的智能，而如果我们在感知机上继续套娃，就可以不断地把原本简单基础的概念组合成更复杂的概念。

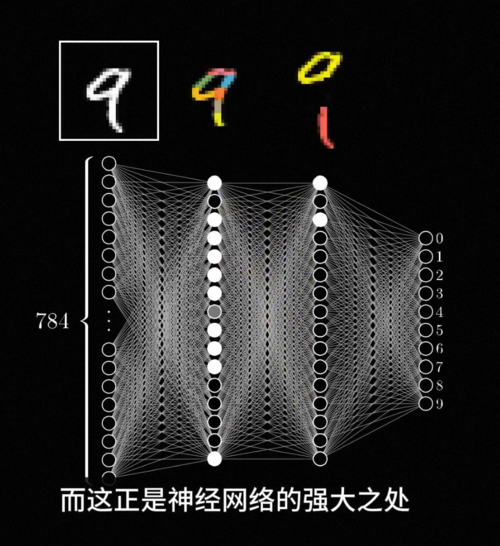
例如在数字识别的这个神经网络中，最前面的神经元就负责识别一些非常基础的笔画和边缘，而往后层的神经元就负责将这些基础的特征组合识别出一些更复杂的概念，比如说圆形横线竖线折线等等，接着更深的神经元可以组合这些线条图形识别出复杂的数字。比如说9就是一个环形加上右下角的尾巴，随着层次的加深，神经网络逐渐从简单的这些特征推导出复杂的整体形态，最终准确地识别一个复杂的概念，而整个这个过程不需要任何人类专家知识的介入，是他自动完成的，而这正是神经网络的强大之处。

随着时间的推移，神经网络的技术也不断的进步，前面我们看到的多层感知机只是最经典最基础的一种，如何设计更好更强大的模型结构一直是深度学习的重要课题，比如真实世界里，动物的视觉神经系统的神经元不需要和前一层的所有神经元全都稠密的连接，而只需要和局部的几个神经元连接就行，而且每个神经元和前一层连接的参数结构又都是类似的。

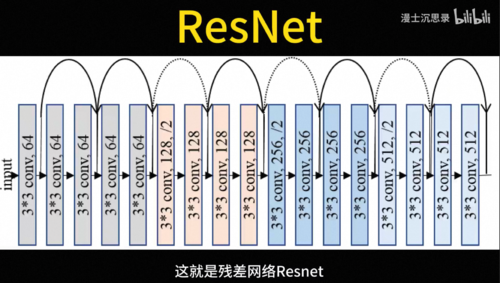
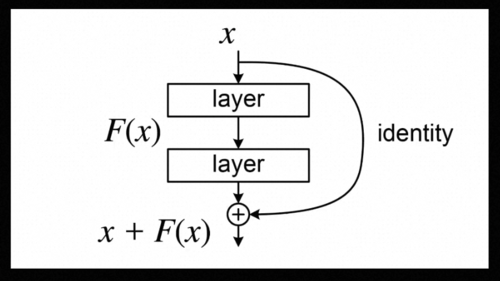
我们设计神经网络的时候也可以借鉴这一点，从而减少参数和运算量提升神经网络的性能，这就是大名鼎鼎的卷积神经网络CNN，后来研究人员发现卷积层堆的多了，训练起来有困难，又增加了一种跳跃式的连接，这就是残差网络ResNet。

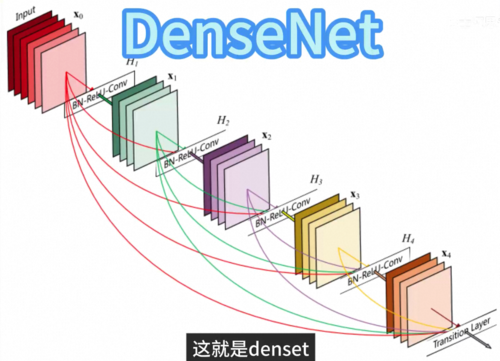
或者你可以把任何两层都跳跃连接起来，这就是danseNet。

再到今天GPT的基础框架Transformer，也就是Attention，它们本质上都是某种网络的基础框架结构，然后有大量的参数需要去决定，一个好的结构可以让黑盒学得更快，需要的数据更少，而这就是深度学习。曾经一个非常重要的领域，神经网络结构设计。

你肯定会问神经网络这么强大，可以自主地发现数据中蕴藏的结构，理解概念，他究竟是怎么做到这一点的呢，答案就是用数据训练，通过奖励和惩罚来引导神经网络形成智能。

那我们应该究竟怎么奖励和惩罚一个神经网络呢，其实从GPT到Alphafold，再到Midjourney和各种强化学习，各种复杂又先进的人工智能模型，几乎无一例外的都在使用着同一种算法来训练网络找到最好的参数，而这个算法就叫做梯度下降。

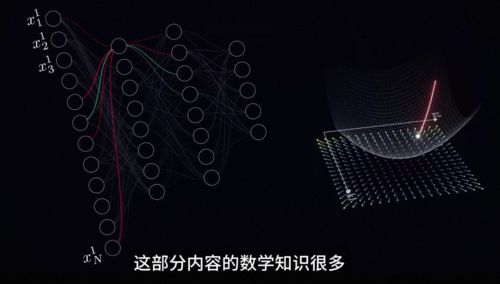
特此说明，这部分内容的数学知识很多，而且技术性很强，但因为它实在是太重要了，所以我们必须要讲。

在讲解梯度下降之前，先让我们简单回顾一下前面的内容，我们首先提到智能的本质是一个黑箱。

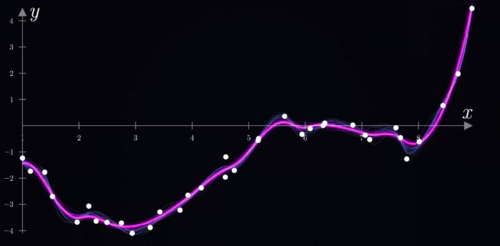
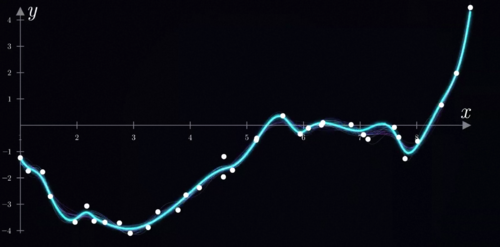
这个黑箱能够从数据中找到输入和输出之间的对应关系，换言之在数据驱动的机器学习和统计学习眼里，所谓的智能本质上就是给你一堆点，然后用一个函数找到你和他们之间的关系罢了，这里的x和y可以是任何你关心的两个量，只要学会了一个可以刻画这些点趋势的函数，我们就可以获得任何一个输入对应的合理输出，换言之实现了智能。

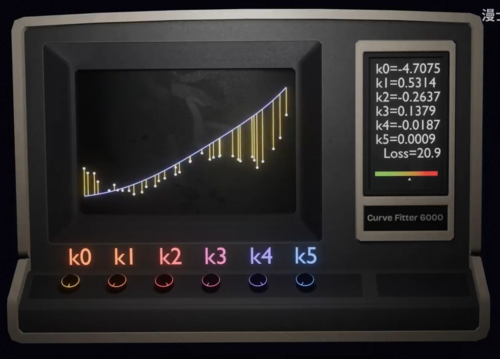
该怎么找到这些数据点所勾勒出的底层规律呢，根据前面的内容，你可能会想到神经网络，这当然是一个办法。不过这里呢，为了理解梯度下降，我们先用一个简单一点的方法找到这个函数，比如说我们线性组合常数x、x平方、X3次方、X4次方、X5次方这几个简单的单项式模块。

换言之，我们想要找到一个五次多项式来刻画这些数据变化的规律，我们需要找到K0到K5

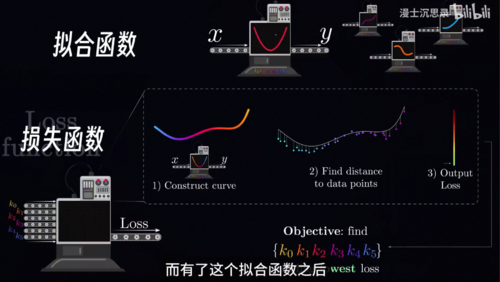
这六个参数最好的组合，那什么样的参数是一个好的组合呢，我们需要一种定量的方式来度量一组系数所对应的多项式，到底拟合的好不好，而这就是损失函数。

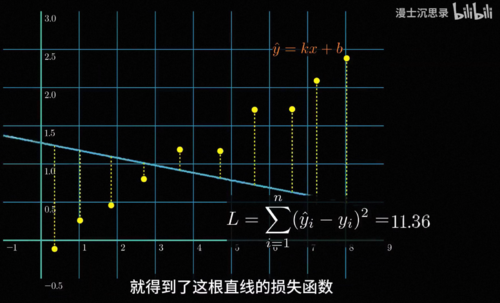
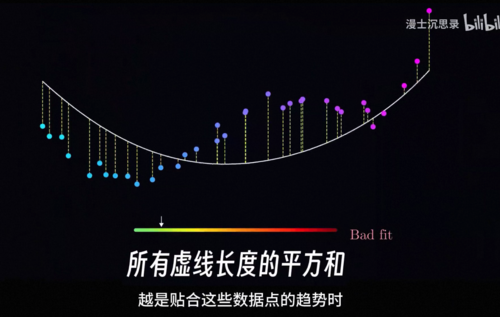
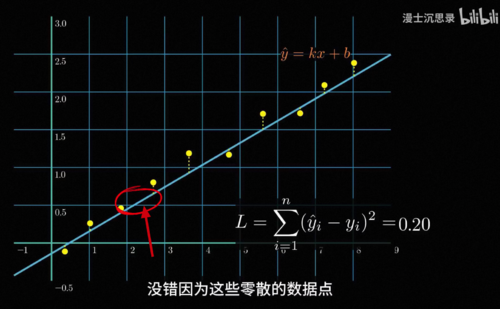
其实大家早就见过损失函数了，中学学过最小二乘法其实就是用一个简单的y等于k，x加b的线性函数来搭建黑箱，对每个数据点线性函数的预测和实际结果都会有偏差，我们把这些偏差的平方加在一起就得到了这根直线的损失函数，在复杂的非线性里损失函数也是一样的道理，我们同样把函数预测的数值和实际数据点的数值误差平方加到一起，就得到了这个函数的损失函数，你可以看到当这个函数的预测越是贴合这些数据点的趋势时，损失函数加在一块就会比较小，而反之损失函数就会比较大。

大体来说损失函数就是在衡量一个模型，预测的和真实的结果之间的偏差程度，只需要记住掌握规律就等于损失函数很小就可以了，请注意这里出现了两种函数，大家不要混淆。第一种是我们用来拟合数据点的这根曲线，我们叫它拟合函数，也就是那个五次多项式，它的输入是x输出是y，我们需要决定这6个参数输入到输出的可能函数有无穷多个，我们想要找到最好的那一个，而什么叫最好呢，为此我们提出了损失函数，它衡量一个拟合函数到底好不好，是一个打分机器，它的输入是多项式的这6个系数，接受到这些系数之后，它会先构造出这个拟合的曲线函数，然后逐以比对计算在所有数据点上的偏差，将它们平方加在一起之后就会得到最终的损失函数的输出了。

我们只需要找到使得这个损失函数很低的输入参数组合K0到K5，我们就可以找到一个出色的拟合函数，而有了这个拟合函数之后，我们就可以把这个拟合函数机器拿过来，输入任何一个我们关心的x得到一个符合数据规律的合理的y，你可以理解为我们在玩这样一个游戏，每一个参数k是一个旋钮，它们通过设置这个系数会产生一个不同的多项式曲线，而你的目标就是调节这些旋钮，让这根拟合函数的曲线和数据点比较贴合。

事实上神经网络干的事情，本质上也是完全一样的，只要把这里的k改成神经元之间的连接系数和预值b，那么训练神经网络同样也是一个调节参数旋钮来降低损失函数的游戏，这个游戏难点在于旋钮实在是太多太多太多了，你看这个5次多样式有6个参数旋钮，已经让人非常头大，而神经网络的参数个数更是多到离谱。

举个例子GPT3一共有1,750亿个参数，换言之你要同时调好1,000多亿个旋钮，并且让这些旋钮组合起来的设置可以有很好的性能，能够跟你对话解决问题，是不是听起来很不可思议呢，这几乎是一件不可能的事情，在数学上这个问题叫做非凸优化求解，它的难度是臭名昭著的大。

这个问题也一度困扰着联结主义的研究者们，也是神经网络这一派研究一直没有真正发展起来非常重要的原因，因为一旦你的模型做大做复杂，你虽然觉得它很强大，但是你找不到好的参数让它实现这种强大，直到后来1976年

由Seppo Linnainmaa提出了一个巧妙的算法：梯度下降，并在1986年由David Rumelhart、Geoffrey Hinton和Ronald Williams共同提出了反向传播算法才算真正解决了这个问题。

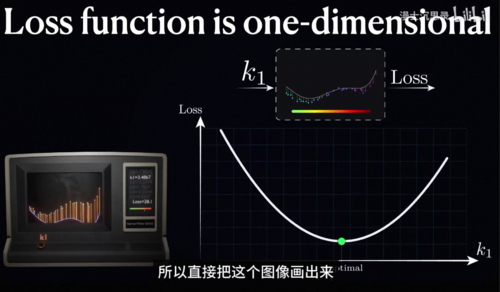
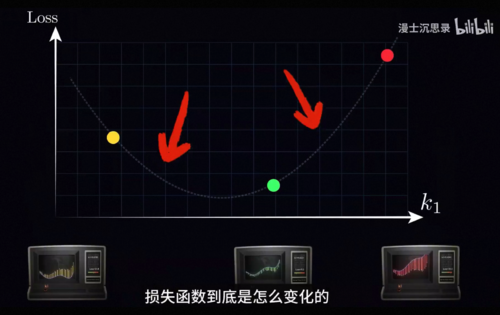
让我们先从最简单的地方开始，假设这里除了K1之外的五个旋钮都已经被固定好了，我告诉你已经有人把它设置在了最好的位置上，现在你只需要去考虑把K1这个旋钮调好，那么到底该怎么办呢，我们可以调节它并观察这个损失函数的变化，此时你会发现损失函数就从原来的6个输入变量变成只有一个变量K1，这是一个一对一变化的函数，我们很容易做图，做出来的图如上图，我们的目标就是找到它的最低点，不过不要被这里的图误导了，我们是解释方便直接把这个图像画出来，但实际上我们并不知道这整个图像，我们知道的只是某一个具体的K1下，这个拟合函数长什么样，然后算出来这个K1对应的损失函数有多大，所以说我们只能得到一系列离散的点，对于每一个输入点

知道函数值是多少，而在这些点中间的位置损失函数到底是怎么变化的我们是全然不知的。

你会发现优化神经网络甚至比求损失函数的最小值更复杂，因为你没有办法看到整个损失函数的全貌，这就好比把你放到了一片地形高低起伏和极其复杂的山地上，每个参数的数值就好比是经纬度，而海拔高度是损失函数的大小，周围大雾弥漫，你只能看到自己脚下的地形，你该如何下山走到一个海拔比较低的地方呢。

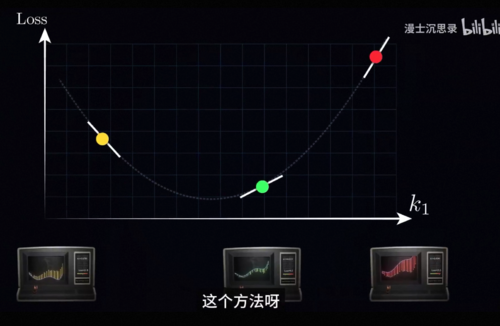
还是用这个K1的例子，刚才我们有一句话说的其实不是很对，那就是我们知道的信息其实还是比纯粹的损失函数大小要多一点，具体来说我们还可以知道在某一个位置下损失函数到底随着K1的增大，是增大还是减小，用数学一点的说法就是我们可以获得损失函数在这一点切线的斜率，更专业的说法是导数。

这个方法大家调洗澡水和收音机的时候其实都用过，那就是你可以把旋钮先往某一个方向转一点点。

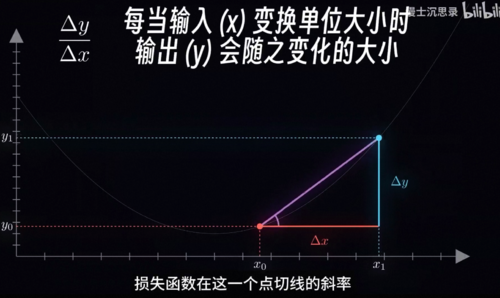
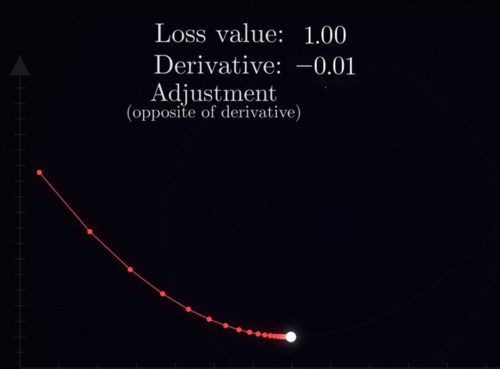
Delta x看看是更好还是更差，比如说这里我们初始在x0的位置，损失函数是y0，然后增加了Delta x到了x1的位置之后，我们再看看损失函数变成了y1，所以我们就会发现损失函数增加了一个Delta y，也就是说它变差了，那这个时候你就知道洗澡水应该往反方向调，所以当我们的调节变化量deltaX无限小的时候，Delta y和Delta x变化量的比值会接近于一个定值，那就是损失函数在这一个点切线的斜率，而这就是函数在这一点的导数在变化很小的时候，函数值y的变化量正比于x的变化量，而这个比值就是导数，所以我们就用一句话来概括一下梯度下降的精神，那就是每次减小一点点我们每次看看要减小损失函数，我们现在的这个位置应该往哪边走，然后就往这个方向走一个很小的距离，接着再看导数再走，不断重复上述流程，这样我们就可以不断的缩小损失函数，直到最后停在底部，参数基本不再变化此时，我们就成功的将损失函数减小到一个很低的程度。

现在我们已经清楚了怎么调节一个旋钮，但这有一个非常不现实的前提，那就是其他5个旋钮已经调到了最优的状态

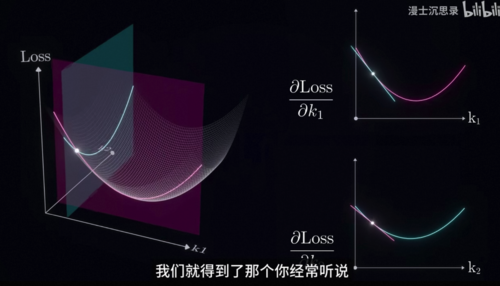
并被固定住，现实中你要同时调节好多旋钮，而且所有的旋钮都没有调好，这个方法有什么用呢，有用。事实上刚才我们的这个方法可以非常容易的拓展到更一般更复杂的情况，比如说假设你现在要同时调节K1和K2两个旋钮，此时损失函数变成一个输入是两个实数，输出是一个实数的二元函数，它可以表示成一个二维的曲面，这就是很多人经常听到的损失曲面。

这里K1、K2的损失曲面看起来就像一个碗，且慢二元函数的导数是个啥呢，现在有两个旋钮，所以调节的方向出现了奇异，到底是只调K1还是只调K2，还是都调呢。这里就涉及到偏导数的概念，我们可以固定K2，只变化K1，此时我们就得到了损失函数对K1的偏导数，反过来固定K1只变化K2，此时就得到了对K2的偏导数，它对应于我们固定K2或者K1当中的一个，然后单独的调节另一个旋钮时对损失函数输出的影响。

几何意义上意味着我们用两个垂直于坐标轴的截面和曲面相交，截面会切出一根曲线来，然后我们再求这根曲线的导数，将这两个导数拼在一起，我们就得到了那个你经常听说但可能不知道是什么的东西-梯度，梯度说白了就是在某个给定位置函数值变化最快的方向，也是曲面在局部最陡峭的方向，是一个二维版本的求导，有了它我们就可以重复刚才的流程，每次向着局部损失函数下降最快的方向前进，我们完全就可以用刚才类似的方法愉快的同时调节两个旋钮了，这个方法就是大名鼎鼎的梯度下降。

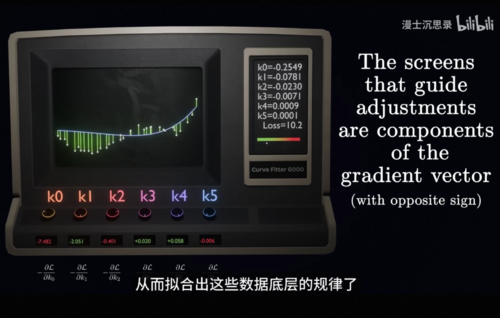
你想既然两个可以，那么这套方法就可以应用到任意多个旋钮，这个问题里完整的损失函数是一个复杂的六维曲面，我们还是可以如法炮制，对每一个旋钮，我们都固定其他的旋钮，然后单独看这个旋钮和损失函数之间，它的变化关系是什么样的，增加它损失函数是增加还是减小，这样我们就能得到每个旋钮的偏导数拼在一起得到了一个6维的梯度，接下来我们只需要让每个旋钮都向着对应的方向不断迭代去减小损失函数，从而拟合出这些数据底层的规律了，现在我们知道梯度下降法可以优化网络，找到损失函数比较低的参数，可是面对一个层层堆叠的非常复杂的神经网络，我们怎么计算出这个梯度呢。

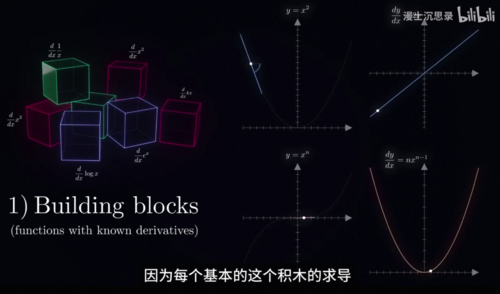
这个问题非常专业，答案是反向传播back propagation，这是一个专门用于计算复杂的神经网络梯度的算法，也是很多人学习深度学习被劝退的第一步，这里我们不详细展开反向传播具体的细节，只告诉你它最精髓的思想，不管是神经网络还是刚才我们的多项式拟合，本质上我们都是用一些非常简单的基础运算，比如说加、减、乘、除、平方、指数之类的不断的组合复合迭代，形成了一个超大的复杂的函数，就像我们用一个个基础的积木一样拼接成一个庞大的机器，我们关心的无非是每个旋钮参数的梯度，用最直白的话说，我们关心每个旋钮动一点点，最后面的损失函数随之变化的关系，而这个信息是可以由后到前层层传递的。

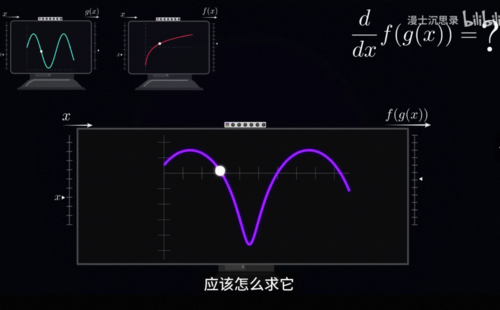
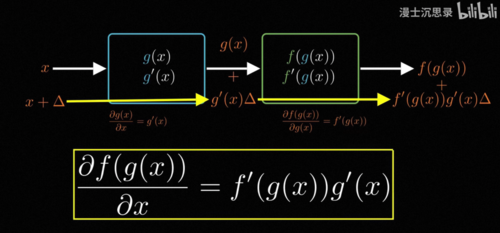
为什么呢，因为每个基本的这个积木的求导，我们都很清楚，而积木在组合过程当中，梯度是怎么样组合变化传递的，我们也很清楚，你看中学我们就学过求导的基础法则，加在一起求导等于各自的导数相加，乘在一起求导则是这个结果，除了上面说的相加和相乘，还有一个最重要的性质，那就是链式法则，如果我们先把一个x送入了一个函数g，再把g(x)这个输出当成输入送入函数f，那么这整个过程合在一块依然是输入一个x，输出一个数值，它也是一个函数，是f(g(x))比如说在这里，如果一个是正弦，一个是log，那么它的图像大概长成这个样子，问题来了，我们知道f和g各自的形式和各自的导数，应该怎么求它这个合体的函数对于x的导数。

那么现在，假设我们把输入x变化一个Delta，根据导数的定义，我们知道第一个g(x)在输入变化Delta的时候，它的输出会变化的比例是g'(x)，所以你就知道这个中间的这个输出g(x)，此时会增加g'(x)乘以Delta，进一步对于后面的这个FX来说，注意到它的导数是f'(g(x))，所以说当它的输入，变化了中间这么大的数值的时候，它的输出就会在中间这个变化量上，进一步乘以f'(g(x))也就是这么大，当我们把右边的这整个除以x的变化量Delta的时候就可以得到链式求导的法则。

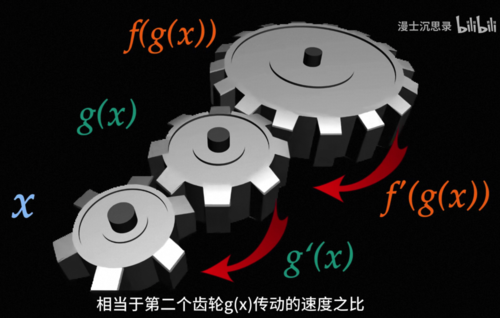
也就是说先做g(x)再做f(x)一起求导，得到的结果是g'(x)乘以f'(g(x))，这就是复合函数的求导，如果用前面积木的比喻，你可以想象有三个齿轮相互咬合。

它们转过的角度就分别代表x，g(x)和f(g(x))，而导数g'(x)就表示第二个齿轮g(x)，相较于第一个齿轮x传动的速度之比，那f'(g(x))就是第三个齿轮，相当于第二个齿轮g(x)传动的速度之比。如果我们想要知道变动一点点，第一个齿轮，第三个齿轮到底变化的速度会有多快，我们就只需要把这两个齿轮的传动比乘在一起就可以了，这就是练式法则。有了练式法则，我们就可以从后往前一步步拆解得到每一个参数的导数，这是因为任何一个参数，从它到损失函数，一定是经过了一系列函数的复合到最后一层输出就是模型预测本身了，我们可以直接计算损失函数以及它的导数，接着我们就可以用刚才的练式法则一层一层从后往前的，把每一层千套这个传导的导函数一步一步的乘在一起，当我们回到最开始K1的位置的时候，就得到了K1相较于整个输出损失函数的梯度，而这个算法就叫做反向传播back propagation。

所以我们最后总结一下，找到这个几百万个旋钮机器最好参数设置的方法，就是用反向传播算法计算出每个参数的导数，接着用梯度下降法每次让这些参数变化一点点，不断地向着更好的参数演化和移动，最后整个神经网络就会神奇的理解，掌握数据中的规律，学会底层函数，并获得这种我们想要的智能。

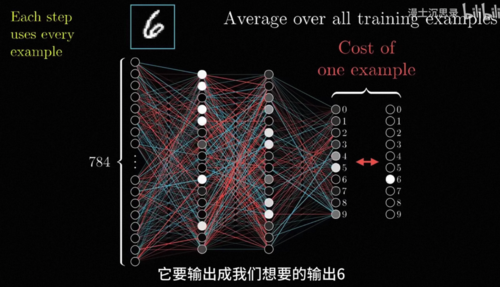
在前面的内容中，我们详细讲解了智能就是搭建黑箱，以及神经网络这个强大，通用的黑箱的构造和由来是什么，还有如何训练一个神经网络，不过这里还有一个非常重要的问题，这个神经网络的黑盒是怎么举一反三的呢，你看我们只是收集了一些数据，然后训练它，在我们收集的数据中对于见过的输入。

比如说这张数字图片，它要输出成我们想要的输出6，那它见过这些东西能够把它正确识别成6并不奇怪，但是对于从来没有见过的其他图片，训练好的网络是怎么能够同时认出其他的数字的呢，这就好比你给一个人做了很多题，它能够把你给他的练习册的题做对，不奇怪，但是他是怎么样学会这些解题的方法，在新的题上考试也能考好的呢。

这个问题其实很深刻，它涉及到机器学习能够成立的一个非常重要的问题-泛化generalization。

这个名词看起来很高端，但正如我们刚才所说的，它的本意就是推广、举一反三、活学活用。

我们还是从前面的最小2乘说起，以及曲线拟合思考这样一个问题，对于中间这个位置输入的x，我们没有任何y的数据，但你还是会觉得它应该就在这个范围里。为什么呢，因为这些零散的数据点勾勒出了一种趋势，当我们用这样的一个连续平滑的函数准确地刻画出这种趋势之后，就可以利用这个函数推测数据中我们没有见过的某一个输入下对应的合理的输出大概应该是多少，这其实就是一种最简单的泛化。

我们将这种关联的趋势理解并且推广到我们没有见过的一些输入数值，通过理解底层规律在未知情境下给出合理的预测和输出，那同样的神经网络也有泛化能力，而且是很强的泛化能力，虽然在训练数据中他没有见过一模一样的图片，但是他可以在训练过程中发现这些输入的图片和标签之间的趋势，和这种微妙的关联性，这种关联就跟我们前面的曲线拟合的时候，中间断开的那一部分看起来应该要这样连线，所以你可以预测那其中的函数值一样，只不过在我们现实的数据里这个趋势可能非常抽象，不如刚才的曲线拟合这么直观，而这正是神经网络强大的地方，你只需要提供数据，那么底层抽象的趋势和规律只需要交给神经网络，他自己学就可以学明白了。

很多行业和学科其实都面临着这类问题，就是不同的情境里有一种感觉和规律，这种感觉和规律难以用简单清晰的数学来计算和描述，比如说围棋里，这一块棋形看起来好不好，能不能活，有经验的棋手一眼能看出来，行话叫做味道不好，但是怎么样学会这种感觉和味道，却非常复杂。还有在说话这个问题上，一句话前面的语境下，后面该接上一个什么样的话，也是一种复杂和微妙的语感，但是怎么学很难说。

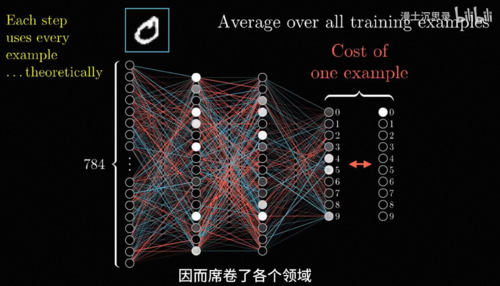
更不用说从氨基酸序列里分析出整个蛋白质结构，这种极为抽象复杂的规律，曾经我们需要非常专业的知识来模仿人类的聪明智慧，而且模仿的还不好，而有了深度学习，你可以不管三七二十一，需要找一个架构合适的神经网络收集数据训练拟合，然后这个神经网络就能领会数据当中你所描述的输入和输出间微妙的联系，并举一反三应用到任何潜在的他没有见过的情景输入中，很多时候做的比人都好，这种公式一样的解决方案非常通用，因而席卷了各个领域引发了这些年的人工智能革命，但是神经网络和深度学习是万能的吗，答案当然是否定的。

每当有一个很厉害的方法可以实现以往不可思议的任务时，人类就有把它当成魔法的倾向，尽管深度学习的确模仿了大脑的神经元结构，但是它和真正的人类智能还有很大的区别，我们都见过这样的梗图：

该怎么区分柴犬和面包，说它们看起来有很多相似之处，比如说都是黄色的呀，长条形的呀等难以区分，这原本是一个玩梗，但对于一切机器学习算法来说，这都是一个根本且致命的问题，因为你看这个模型，它一直就是通过各种图像的特征输入，和你要它的这个标签来理解图片的内容的，所以它在训练当中所理解的事情就是一个黄色的长条形的物体是面包。

因此当你给它一个在训练集以外的柴犬，图片时它会因为这个柴犬符合面包的各种特征而产生错误的判断，这本质上是概念之间的相关性和因果关系之间微妙的区别，他没有把握，而这个问题在收集数据训练模型的这一套方法论中永远无法避免，这就是为什么有很多用神经网络、算命或者预测犯罪几率的应用广受批评，因为模型会错误的把数据集里的共同出现当成必然联系，比如说看到黑人就觉得一定会犯罪这个样子，更糟糕的是你可能永远不知道

强大的神经网络黑盒究竟领会了什么神秘的联系，因为神经网络太过强大和复杂，所以我们几乎无法理解它的内部是如何运作，给出我们想要的合理预测的。

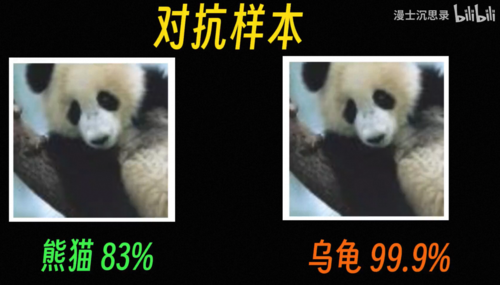
一个典型的例子是对抗样本，这是两张图片你能看出它们有什么区别吗，但如果让一个准确率非常高的最先进的神经网络来看，第一张图片他觉得是熊猫，但第二张图片他以99%的信心认为是一只乌龟，仔细看你会发现第二张图片相较于第一张添加了一些十分微小的噪声，而这些噪声可不是乱来的，他经过了特别的设计专门用来欺骗神经网络，这种图片就叫做对抗样本。

对于它的理解和研究直到现在还在进行，而我们依然没有彻底理解它，大家一般认为它触发了神经网络底层某些神奇的开关，这些在人眼看来杂乱无章的噪声，在神经网络看来却有着强烈的乌龟的特点和相关性，看到这里你还觉得神经网络无所不能吗。