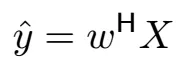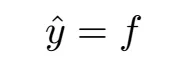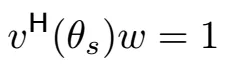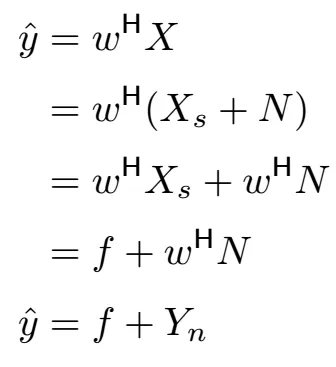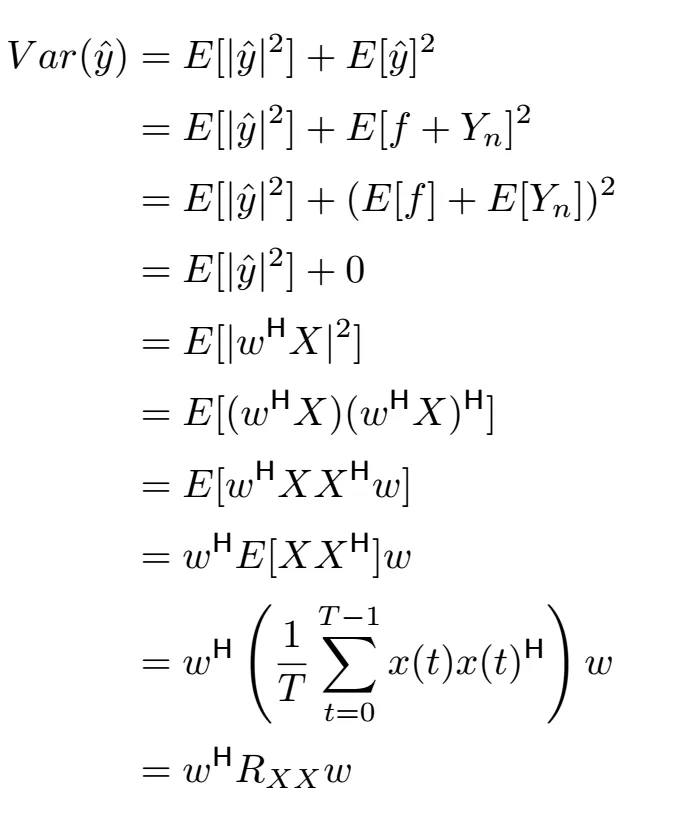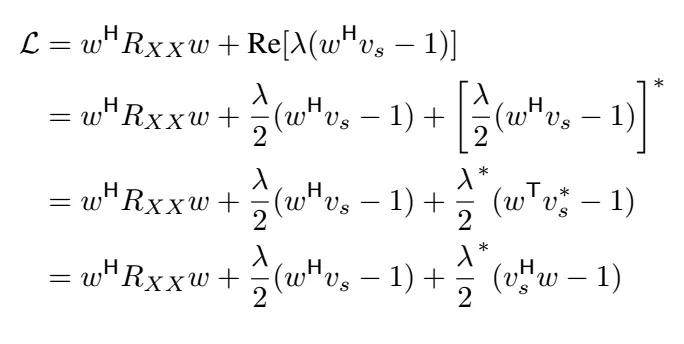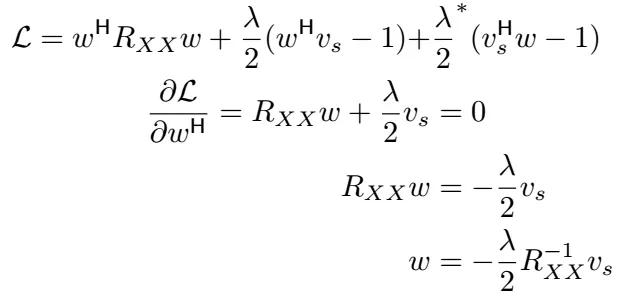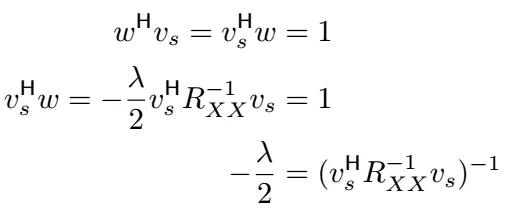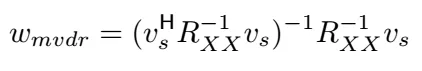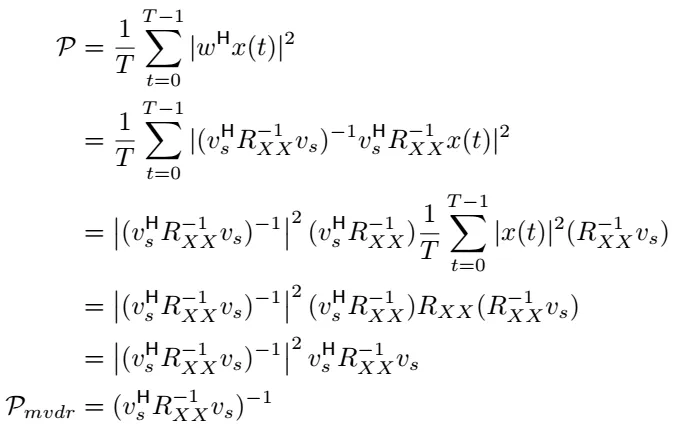照片由 Vidar Nordli-Mathisen 拍摄，来自 Unsplash。

在这篇文章中，我们将推导和实现Capon波束形成器，这是一项阵列处理技术，它可以帮助我们估算信号的到达角度，并且低失真地重建这些信号。这项技术常用于雷达、地震学、声呐以及其他使用传感器网络的应用。本文是介绍波束成形器系列的一部分。

• 波束成形介绍（第一部分）——延迟求和波束成形器
• 波束成形介绍（第二部分）——Bartlett波束成形器
• 波束成形介绍（第三部分）——Capon波束成形器（这一篇）
• 波束成形介绍（第四部分）——方向定位与信号恢复

波束成形是一种阵列处理技术，用于从不同方向到达的信号进行空间滤波处理。在Bartlett波束成形教程，尽管信号在时间和频率上受到了严重干扰，我们也可以根据信号的到达方向恢复所需的信号。

自适应波束成形根据当前信号环境的统计特性计算权重，通过这些权重，我们可以恢复信号。信号模型与Bartlett教程中的相同，这里简要回顾一下。我们假设使用具有N个元素的均匀线性阵列(ULA)，接收T个时间样本数据。

在本节中，我们将推导出通常也称为最小方差无失真响应（MVDR）波束形成器的Capon波束形成器。这个估计器旨在最小化信号方差，我们将从理想波束形成器出发建立问题框架、设定约束条件，并提出一个优化问题以实现这一自适应技术。

让我们回顾一下一般波束形成器 w，我们对收到的信号 X 进行矩阵运算处理。

我们可以对 w 加一个约束，使得数组输出 ŷ 精确等于原始信号 f。

恢复的信号与原始信号完全相同（即没有失真），这种情况叫做无失真响应。现在，如果w实际等于真实的信号导向向量v（θₛ），那么它们的内积将等于1。我们可以用以下表达式来重新表述这一限制条件。

这是我们对 波束形成器 w 的 不失真约束条件。这实际上做了两件事，首先它确保波束形成器在真实信号方向上的响应能量较高，以此来使其指向该方向。其次，它确保在所有其他方向上的响应能量都很低，这有时称为在所有其他方向上 导向零点。这种方法的缺点在于，我们的波束形成器仅针对单一信号设计，因为我们在这个模型中只考虑了一个信号。现在让我们来看看该波束形成器的输出，以便构建目标函数。

让我们将无失真的响应加入到通用波束形成器中，并检查其在带有噪声信号下的响应，其中 X = Xₛ + N。这里，N 是一个均值为零的加性高斯白噪声（Additive Gaussian White Noise, AWGN）。

我们有原始信号 f 加上处理过的噪声项 Yₙ，这个额外的噪声项会导致我们的估计值出现误差。我们需要找到一种方法来减少这种噪声，以保持准确的估计值。噪声的强度可以通过其方差来描述，因此我们的目标可以表述为最小化噪声的方差。但有一个问题，我们无法单独获取信号和噪声，而只能同时得到它们的组合。因此我们需要最小化总响应 ŷ（即我们能够获取的项）的方差，以便使我们的估计值准确。现在让我们来把这拼凑起来，我们的响应在没有噪声的情况下是无失真的，这意味着我们需最小化无失真的响应的方差。

由于我们要最小化无失真的响应的方差，让我们来看看这个方差项实际上是怎么样的。下面，我们来简化无失真响应 ŷ 的方差。

在第4行，我们利用了f和Yₙ均值为零的条件，经过一些变换后，我们得到了与Bartlett波束形成器相同的表达式。其中Rₓₓ是(NxN)的厄米特样本相关矩阵，而w是用于恢复信号的波束形成权重。除了这个表达式是我们将要最小化的优化目标，其受限条件为不失真约束条件。

我们现在来推导一下Capon波束形成器，这部分涉及大量数学的内容，所以如果你想跳过这部分，可以直接跳到结果部分，所有重要的概念和直觉都在前面的部分中。这是优化问题：

我们使用拉格朗日乘数来处理无失真约束条件，但需要记住拉格朗日函数是一个实数表达式，尽管拉格朗日乘数自身是复数（由于我们的约束是复数）。为了应对这种情况，我们利用性质 Re[2z] = z + z（其中 z 表示 z 的共轭复数），其中 z 是一个复数。下面展示带有复数拉格朗日乘数的扩展目标函数。

下面的表述是正确的，参考书目为《统计信号处理 第1卷》（Statistical Signal Processing Vol 1）（第15.6章），但我省略了一些步骤，直接跳到了拉格朗日乘数法，如需深入了解复数拉格朗日乘数的扩展方法，请参阅该书。

趣味事实：复数变量的导数称为Wirtinger 导数。

现在我们来解决这个问题吧，我们对 w ᴴ 求偏导，并让表达式等于零。

术语 -λ/2 是一个复数标量，我们现在用这个约束来求解它。

现在代入拉格朗日乘数，我们得到了其MVDR（Capon）波束形成器的最终表达形式为：

（Nx1）的权重向量 w 估计在给定方向上的信号，我们可以利用功率表达式来估计功率，通过将Beamformer插入其中，利用方差和功率之间的关系，正如我们在Bartlett Beamformer中所做的一样。

现在我们有了波束形成器的最终公式，看看它是如何工作的。

这将与波束形成器的Bartlett代码非常相似，实际上，Bartlett波束形成器和Capon波束形成器的代码都包含在同一笔记本中，大部分代码将与第二部分中的代码重复，因此这里很多内容可能不再赘述。让我们从一些辅助函数开始吧，完整的笔记本在GitHub。

    # 生成具有默认间距为0.5波长的指向矢量  
    steering_vector = lambda theta, N, d=0.5 : np.exp(-2j * np.pi * d * np.arange(N) * np.sin(theta))   

    # 将dB转换为瓦特和将瓦特转换为dB  
    db2watt = lambda db : 10**(db/10)  
    watt2db = lambda watt : 10*np.log10(watt)  

    # 参考链接: https://github.com/morriswmz/doatools.py/blob/master/doatools/utils/math.py  
    def randcn(shape):  
        """从复高斯分布中采样生成。  

        参数:  
            shape (形状（输入元组）): 输出的形状。  

        返回:  
            numpy.ndarray: 包含样本的复数numpy数组。  
        """  
        x = 1j * np.random.randn(*shape)  
        x += np.random.randn(*shape)  
        x *= np.sqrt(0.5)  
        return x 

这里是我们将输入的参数模型。我们再一次通过从所有源信号的平均值中减去信号的信噪比来确定噪声功率水平。

    # 输入参数  
    SNR = 15.0 # 假设所有信号的信噪比(SNR)相同（最大值：100，最小值：0）  
    T = 10000  # 样本数  
    M = 10     # 阵元数量  
    D = 3      # 信号源数量  
    THETA_DEG = [-25, 25, 30] # 到达角度  
    SOURCE_POWER = np.array([20, 17, 23]) # 以dB表示的功率  

    # 衍生参数  
    SOURCE_POWER_WATT = db2watt(SOURCE_POWER)  
    NOISE_POWER_DB = SOURCE_POWER.mean() - SNR  
    NOISE_POWER_WATT = db2watt(NOISE_POWER_DB)  
    SOURCE_THETAS = [theta*np.pi/180 for theta in THETA_DEG] # 转换成弧度

下面我们就来讲讲信号模型。

    # 构造阵列响应  
    V = np.vstack([steering_vector(theta, M) for theta in 源θ值]).T  

    # 获取随机源信号   
    C = np.eye(D)*源功率 # 源协方差  
    F = C @ randcn((D, T))  

    # 复数AWGN噪声  
    N = 噪声功率 * randcn((M, T))  

    # 构造信号X  
    X = V @ F + N

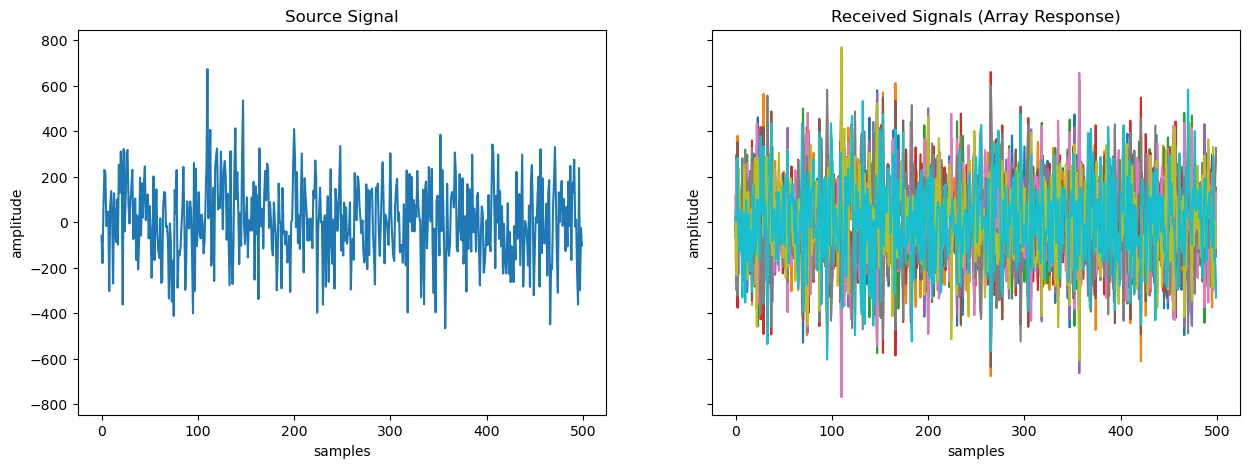
我们构建了三个信号，其中有两个信号的到达角非常接近，以此来展示Capon波束形成器的能力。这些信号已在下方图表中展示了，左边的图显示单个源信号，右边的图显示所有源信号和噪声的阵列响应 X。我们将用Capon波束形成技术来估计到达方向并恢复源信号。

图1。左图显示单一信号源，右图显示三个信号源的阵列响应。（作者提供）

注意：我们的模型将零均值随机向量作为源信号，但我们也可以使用正弦信号。在第4部分，我们将看到如何生成和处理正弦信号。

就像 Bartlett 方法一样，我们将遍历包含不同角度值的向量，并计算当前角度下的功率响应以及恢复信号。具有最高功率响应的角度最有可能是信号，如果需要的话，我们也能够得到恢复信号。但在这样做之前，让我们先计算信号样本相关矩阵 Rₓₓ 的逆矩阵并保存下来。

Rxx = (X @ np.conj(X).T) / X.shape[1]  # 计算共轭转置矩阵并除以X的列数
Rxx_inv = np.linalg.pinv(Rxx + 1e-6*np.eye(Rxx.shape[0]))  # 计算广义逆矩阵，加入小的单位矩阵以避免奇异矩阵问题
# 计算Rxx的形状和Rxx_inv的形状
Rxx.shape, Rxx_inv.shape

现在让我们一个个来看看这些角度，看看会得到什么：

    # 需要处理的角度范围  
    thetas = np.arange(-90, 90 + 0.1, 0.1)  

    outputs = {"bartlett" : [], "capon" : []}  
    responses = {"bartlett" : [], "capon" : []}  

    for _theta in thetas:  
        _theta *= np.pi/180  
        v = steering_vector(_theta, M) # 导向矢量  

        # Bartlett波束形成器  
        pb = np.conj(v)[:, None].T @ Rxx @ v  
        wb = v / M # 使用归一化导向矢量  

        # Capon波束形成器  
        pc = 1/(np.conj(v)[:, None].T @ Rxx_inv @ v)  
        wc = (Rxx_inv @ v)[:, None] * pc  

        # （可选）估计实际信号  
        yb = (wb.conj().T @ X)  
        yc = (wc.conj().T @ X)  

        # 追加到输出结果列表  
        outputs["bartlett"].append(yb.squeeze())  
        outputs["capon"].append(yc.squeeze())  

        # 转换为分贝（5*log10(x)）  
        responses["bartlett"].append(5*np.log10(np.abs(pb)))  
        responses["capon"].append(5*np.log10(np.abs(pc)))  

    # 标准化响应  
    responses["bartlett"] -= np.max(responses["bartlett"])   
    responses["capon"] -= np.max(responses["capon"])   

    # 找到响应最大的角度  
    angle_idx_b = np.argmax(responses["bartlett"])  
    aoa_b = thetas[angle_idx_b]  
    s_hat_b = outputs["bartlett"][angle_idx_b]  # 估计的信号值  

    angle_idx_c = np.argmax(responses["capon"])  
    aoa_c = thetas[angle_idx_c]  
    s_hat_c = outputs["capon"][angle_idx_c]  # 估计的信号值

到达角估计

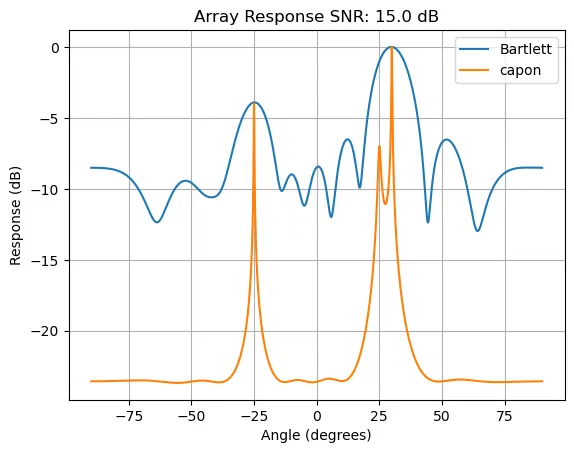
这里对比一下Bartlett和Capon在到达角估计上的方法：

图2. Bartlett和Capon波束形成的空间谱输出。来源：本文作者

你看，Capon波束形成器的噪声水平低很多，并且没有旁瓣。它能够分别分辨出在25度和30度到达的两个相邻的信号，而Bartlett波束形成器则无法做到这一点。信号噪声比（SNR）设置为15dB，如果SNR太低，则两个相邻的信号将不再被Capon波束形成器分辨。试着调整输入参数，看看波束形成器的输出会有哪些变化，我建议每次只改一个参数。

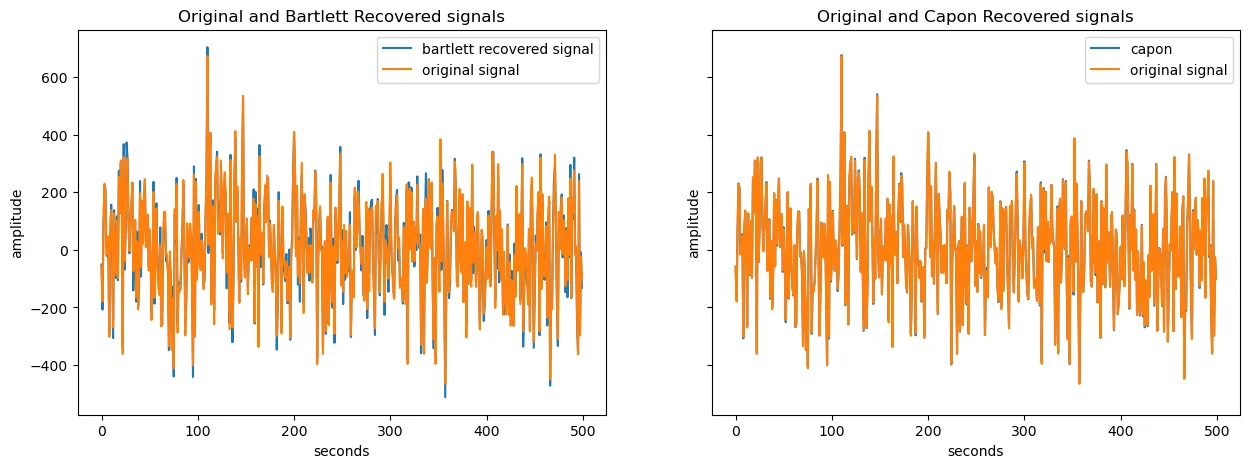
这里是一条已恢复信号的波形图，你可以在笔记本中查看其他信号。如果信噪比足够高，你应该都能识别所有信号。

图3. 恢复的信号图。左图：巴特勒，右图：卡彭。作者提供。

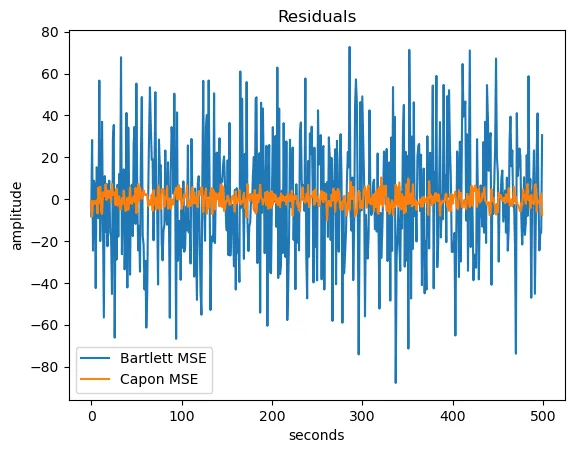
一般来说，波束形成器是一种空间滤波器（Spatial filter），它允许我们区分并恢复来自不同方向的信号。我们来检查一下均方误差性能，并看看残差（真实信号和恢复信号之间的差距）。

    bartlett_res = F[source_num, :plot_samples].real - outputs["bartlett"][角度索引_bartlett].real[:plot_samples]  
    bartlett_mse = np.mean((bartlett_res)**2)  

    capon_res = F[source_num, :plot_samples].real - outputs["capon"][角度索引_capon].real[:plot_samples]  
    capon_mse = np.mean((capon_res)**2)  

    bartlett_mse, capon_mse  
    # 856.8309654845407, 13.906399082018092

图4. 原始信号与恢复信号之间的差异。来源：（作者）

我们引入了Capon波束成形器，这是一种强大的阵列处理算法，它能让我们准确地估计信号的到达角度，并以最小失真重构信号。与Bartlett波束形成器相比，它提供了更高的角度分辨能力，能够区分间隔紧密的信号，但需要进行矩阵求逆，计算量更大。在第四部分里，我们将使用正弦信号提供一个更实用的教程。

• Van Trees, H. L. (2002). 最优阵列处理：检测、估计与调制理论（第四部分）. Wiley.

• Kay, S. M. (1993). 统计信号处理基础：估计理论. Prentice-Hall.

• https://math.stackexchange.com/questions/1182625/lagrangian-multipliers-in-complex-optimization （关于复数优化中的拉格朗日乘数的讨论）

• https://www.youtube.com/watch?v=xYpjSO3L6kw&t=620s （视频链接，时长：620秒之后）