Problem: 337. 打家劫舍 III

1. 思路

2. 解题方法

   1. 后序遍历（递归）

3. 复杂度

4. Code

思路

题目特点： 1）输入：树 2）动态规划

解题方法

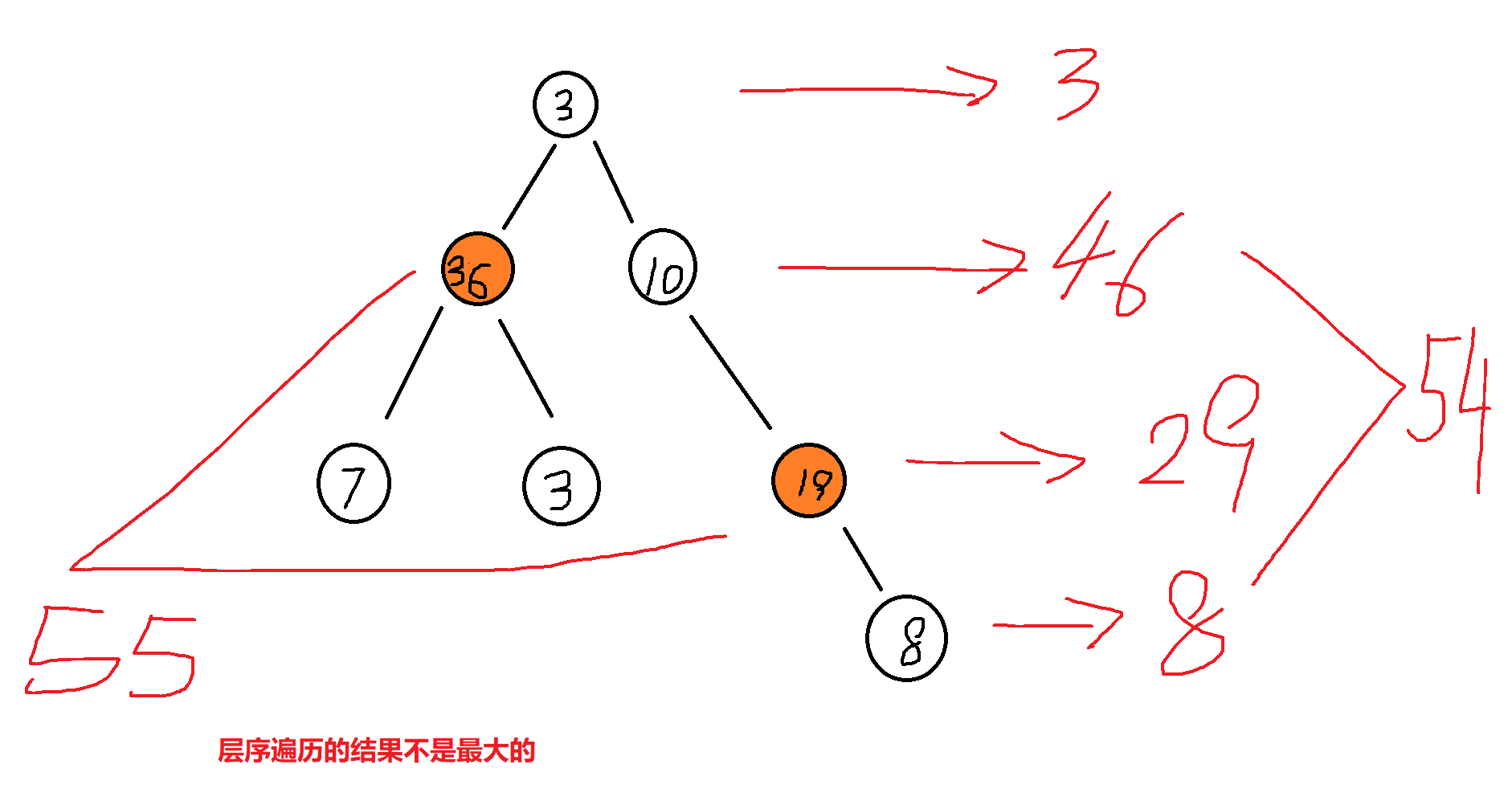
1、观察两个示例，发现小偷偷树形结构的小区，不能在相邻层偷。（注意：不是隔一层偷，我一开始的错误理解是小偷只能隔着一层偷，我容易产生固有的印象）

2、由于要一层一层去看怎么偷，则需要去遍历树。第二步，要判断遍历树的方法：前中后序和层序遍历。

通过举例子，可以排除层序遍历。

3、因为要对比下一层和上一层，且应该先计算出子树的最大值，再计算当前层的最大值，所以应使用后序遍历。

后序遍历（递归）

1、确定递归函数的参数和返回值 1）每次要记录的有两个状态：一个是偷当前节点计算得出的最大值，另一个是不偷当前节点计算得出的最大值。则返回值应使用一个数组，去保存这两个最大值。 2）参数：TreeNode root

2、确定递归函数的终止条件 1）如果你写过书店前中后序遍历，很明显：if (root == null) return [0,0];

3、确定递归函数的单层逻辑 1）分为两种情况：第一种：root==null，上面已经分析过。第二种：root != null

先计算出子树的最大值，再计算当前层的最大值

List<Integer> result = new ArrayList<>(); // 也可以用new int[2];

List<Integer> left = robTree(root.left);
List<Integer> right = robTree(root.right);

// 计算偷当前节点的最大值
int val1 = root.val + left.get(0) + right.get(0);
// 计算不偷当前节点的最大值
int val2 = Math.max(left.get(0), left.get(1)) + Math.max(right.get(0), right.get(1));

result.add(val2);
result.add(val1);

复杂度

• 时间复杂度: O(n)O(n)

• 空间复杂度: O(log2(n))O(log_2(n))【递归栈的空间】

Code

/**
 * Definition for a binary tree node.
 * public class TreeNode {
 *     int val;
 *     TreeNode left;
 *     TreeNode right;
 *     TreeNode() {}
 *     TreeNode(int val) { this.val = val; }
 *     TreeNode(int val, TreeNode left, TreeNode right) {
 *         this.val = val;
 *         this.left = left;
 *         this.right = right;
 *     }
 * }
 */
class Solution {
    /**
     * 树形dp的入门题
     *
     * 1、确定递归函数的参数和返回值
     * public List<Integer> robTree(TreeNode root)
     * dp[i]的含义
     * dp数组（dp table）以及下标的含义：下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。
     * 
     * 2、确定终止条件
     * if (root == null) return [0,0]; //伪代码
     * 
     * 3、确定遍历顺序
     * 树的后序遍历
     *
     * 4、确定单层递归的逻辑
     * 计算偷和不偷当前节点的最大金钱
     *
     * @param root
     * @return
     */
    public int rob(TreeNode root) {
        List<Integer> result = robTree(root);
        return result.get(0) > result.get(1) ? result.get(0) : result.get(1);
    }

    /**
     * 下标为0记录不偷该节点所得到的的最大金钱，下标为1记录偷该节点所得到的的最大金钱。
     * @param root
     * @return
     */
    public List<Integer> robTree(TreeNode root) {
        List<Integer> result = new ArrayList<>();
        result.add(0);
        result.add(0);
        if (root != null) {
            // 通过递归左节点，得到左节点偷与不偷的金钱。
            List<Integer> left = robTree(root.left);

            // 通过递归右节点，得到右节点偷与不偷的金钱。
            List<Integer> right = robTree(root.right);

            int val1 = root.val + left.get(0) + right.get(0);
            // 不偷cur，那么可以偷也可以不偷左右节点，则取较大的情况
            int val2 = Math.max(left.get(0), left.get(1)) + Math.max(right.get(0), right.get(1));

            // 不偷左孩子和右孩子
            result.set(0, val2);
            result.set(1, val1);
        }
        return result;
    }
}