阅读本文需要的背景知识点：岭回归、Lasso回归、一点点编程知识

一、引言

  前面学习了岭回归与Lasso回归两种正则化的方法，当多个特征存在相关时，Lasso回归可能只会随机选择其中一个，岭回归则会选择所有的特征。这时很容易的想到如果将这两种正则化的方法结合起来，就能够集合两种方法的优势，这种正则化后的算法就被称为弹性网络回归¹ （Elastic Net Regression）

二、模型介绍

  弹性网络回归算法的代价函数结合了Lasso回归和岭回归的正则化方法，通过两个参数 λ 和 ρ 来控制惩罚项的大小。

$$\mathrm{Cost}(w)=\sum _{i=1}^N{\left(y_i-w^T{x}_i\right)}^2+\lambda \rho \Vert w{\Vert }_1+\frac{\lambda (1-\rho )}{2}\Vert w{\Vert }_2^2$$

  同样是求使得代价函数最小时 w 的大小：

$$w=\underset{w}{\mathrm{argmin}}\left(\sum _{i=1}^N{\left(y_i-w^T{x}_i\right)}^2+\lambda \rho \Vert w{\Vert }_1+\frac{\lambda (1-\rho )}{2}\Vert w{\Vert }_2^2\right)$$

  可以看到，当 ρ = 0 时，其代价函数就等同于岭回归的代价函数，当 ρ = 1 时，其代价函数就等同于 Lasso 回归的代价函数。与 Lasso 回归一样代价函数中有绝对值存在，不是处处可导的，所以就没办法通过直接求导的方式来直接得到 w 的解析解，不过还是可以用坐标下降法²（coordinate descent）来求解 w。

三、算法步骤

坐标下降法：

  坐标下降法的求解方法与 Lasso 回归所用到的步骤一样，唯一的区别只是代价函数不一样。

  具体步骤：

（1）初始化权重系数 w，例如初始化为零向量。

（2）遍历所有权重系数，依次将其中一个权重系数当作变量，其他权重系数固定为上一次计算的结果当作常量，求出当前条件下只有一个权重系数变量的情况下的最优解。

  在第 k 次迭代时，更新权重系数的方法如下：

KaTeX parse error: Expected & or \\ or \end at position 23: …{matrix} w_m^k 表̲示第k次迭代，第m个权重系数 …

（3）步骤（2）为一次完整迭代，当所有权重系数的变化不大或者到达最大迭代次数时，结束迭代。

四、代码实现

使用 Python 实现弹性网络回归算法（坐标下降法）：

def elasticNet(X, y, lambdas=0.1, rhos=0.5, max_iter=1000, tol=1e-4):
    """
    弹性网络回归，使用坐标下降法（coordinate descent）
    args:
        X - 训练数据集
        y - 目标标签值
        lambdas - 惩罚项系数
        rhos - 混合参数，取值范围[0,1]
        max_iter - 最大迭代次数
        tol - 变化量容忍值
    return:
        w - 权重系数
    """
    # 初始化 w 为零向量
    w = np.zeros(X.shape[1])
    for it in range(max_iter):
        done = True
        # 遍历所有自变量
        for i in range(0, len(w)):
            # 记录上一轮系数
            weight = W[i]
            # 求出当前条件下的最佳系数
            w[i] = down(X, y, w, i, lambdas, rhos)
            # 当其中一个系数变化量未到达其容忍值，继续循环
            if (np.abs(weight - w[i]) > tol):
                done = False
        # 所有系数都变化不大时，结束循环
        if (done):
            break
    return w

def down(X, y, w, index, lambdas=0.1, rhos=0.5):
    """
    cost(w) = (x1 * w1 + x2 * w2 + ... - y)^2 / 2n + ... + λ * ρ * (|w1| + |w2| + ...) + [λ * (1 - ρ) / 2] * (w1^2 + w2^2 + ...)
    假设 w1 是变量，这时其他的值均为常数，带入上式后，其代价函数是关于 w1 的一元二次函数，可以写成下式：
    cost(w1) = (a * w1 + b)^2 / 2n + ... + λρ|w1| + [λ(1 - ρ)/2] * w1^2 + c (a,b,c,λ 均为常数)
    => 展开后
    cost(w1) = [aa / 2n + λ(1 - ρ)/2] * w1^2 + (ab / n) * w1 + λρ|w1| + c (aa,ab,c,λ 均为常数)
    """
    # 展开后的二次项的系数之和
    aa = 0
    # 展开后的一次项的系数之和
    ab = 0
    for i in range(X.shape[0]):
        # 括号内一次项的系数
        a = X[i][index]
        # 括号内常数项的系数
        b = X[i][:].dot(w) - a * w[index] - y[i]
        # 可以很容易的得到展开后的二次项的系数为括号内一次项的系数平方的和
        aa = aa + a * a
        # 可以很容易的得到展开后的一次项的系数为括号内一次项的系数乘以括号内常数项的和
        ab = ab + a * b
    # 由于是一元二次函数，当导数为零是，函数值最小值，只需要关注二次项系数、一次项系数和 λ
    return det(aa, ab, X.shape[0], lambdas, rhos)

def det(aa, ab, n, lambdas=0.1, rhos=0.5):
    """
    通过代价函数的导数求 w，当 w = 0 时，不可导
    det(w) = [aa / n + λ(1 - ρ)] * w + ab / n + λρ = 0 (w > 0)
    => w = - (ab / n + λρ) / [aa / n  + λ(1 - ρ)]

    det(w) = [aa / n + λ(1 - ρ)] * w + ab / n  - λρ = 0 (w < 0)
    => w = - (ab / n - λρ) / [aa / n  + λ(1 - ρ)]

    det(w) = NaN (w = 0)
    => w = 0
    """
    w = - (ab / n + lambdas * rhos) / (aa / n + lambdas * (1 - rhos))
    if w < 0:
        w = - (ab / n - lambdas * rhos) / (aa / n + lambdas * (1 - rhos))
        if w > 0:
            w = 0
    return w

五、第三方库实现

scikit-learn³ 实现：

from sklearn.linear_model import ElasticNet

# 初始化弹性网络回归器
reg = ElasticNet(alpha=0.1, l1_ratio=0.5, fit_intercept=False)
# 拟合线性模型
reg.fit(X, y)
# 权重系数
w = reg.coef_

六、动画演示

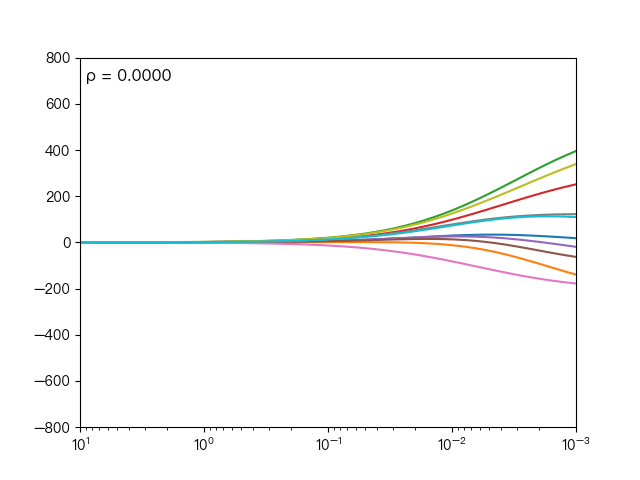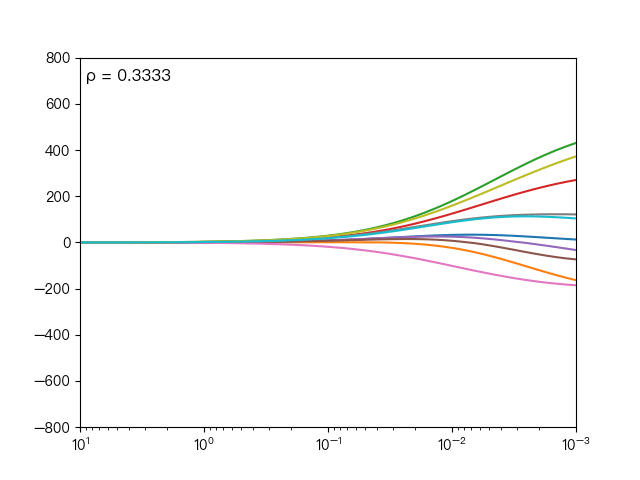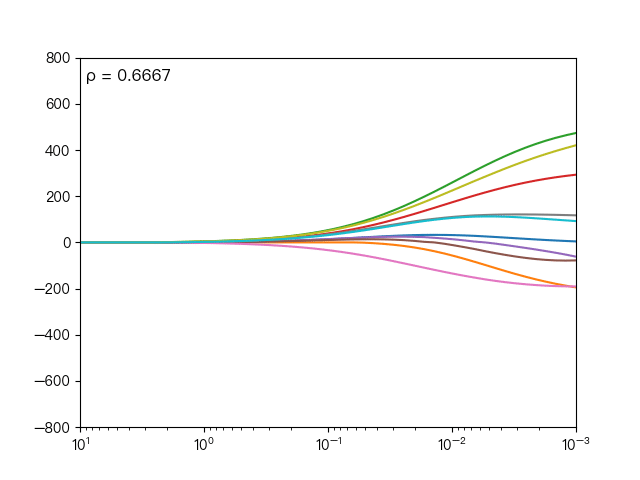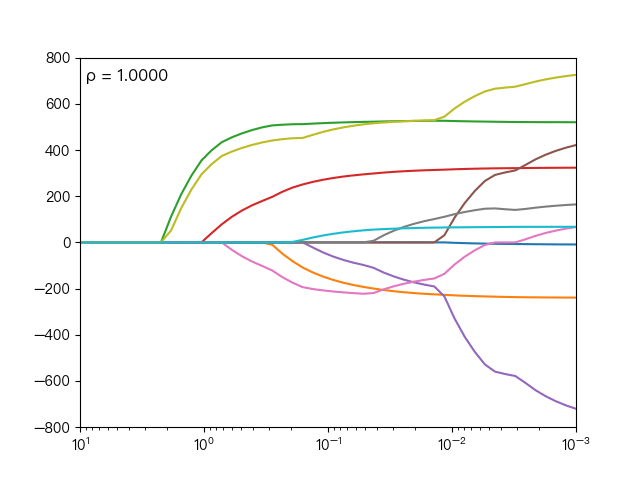
  下面动图展示了不同的 ρ 对弹性网络回归的影响，当 ρ 逐渐增大时，L1正则项占据主导地位，代价函数越接近Lasso回归，当 ρ 逐渐减小时，L2正则项占据主导地位，代价函数越接近岭回归。

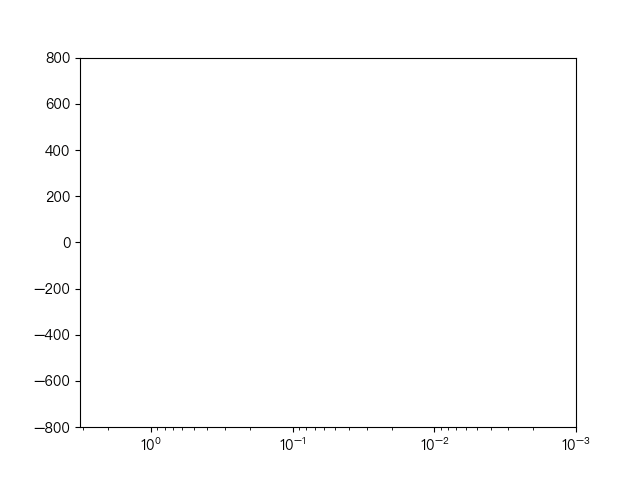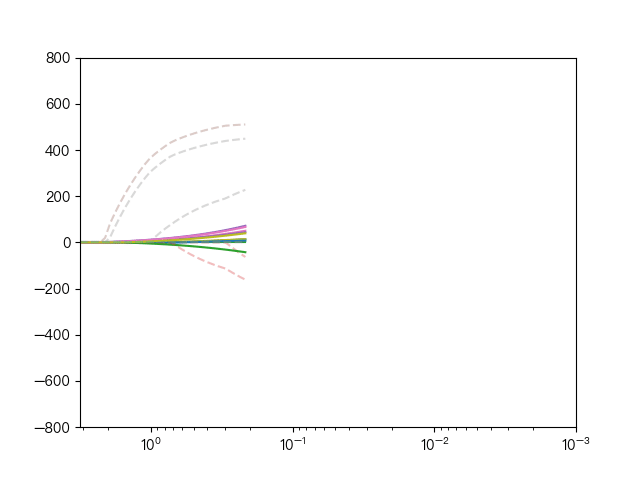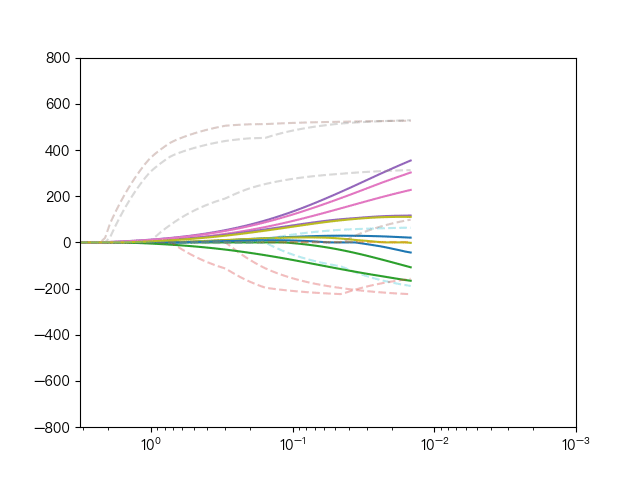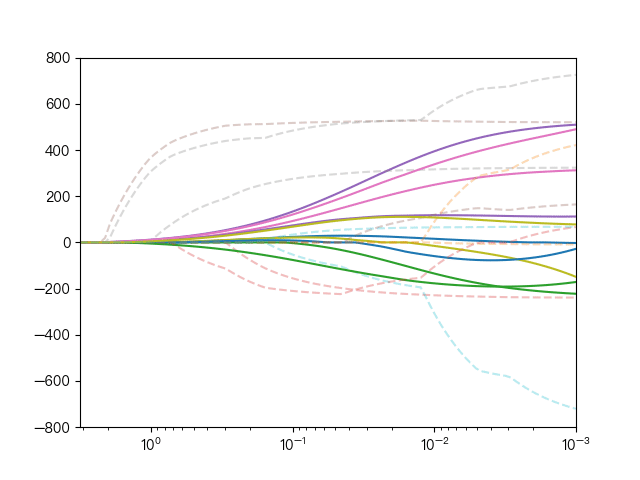
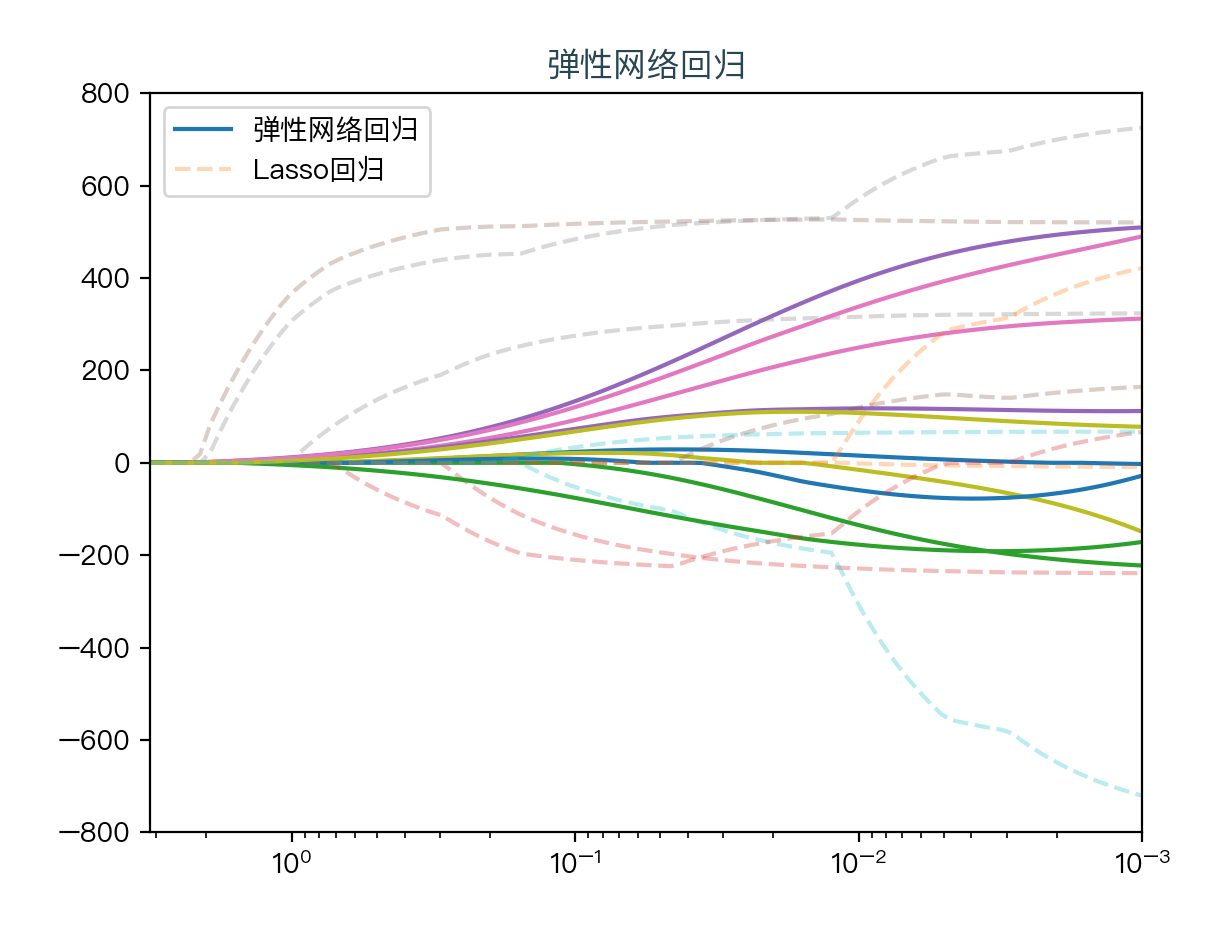
  下面动图展示了Lasso回归与弹性网络回归对比，虚线表示Lasso回归的十个特征，实线表示弹性网络回归的十个特征，每一个颜色表示一个自变量的权重系数（训练数据来源于sklearn diabetes datasets）

  可以看到弹性网络回归相对Lasso回归来说，保留了Lasso回归的特征选择的性质，又兼顾了岭回归的稳定性。

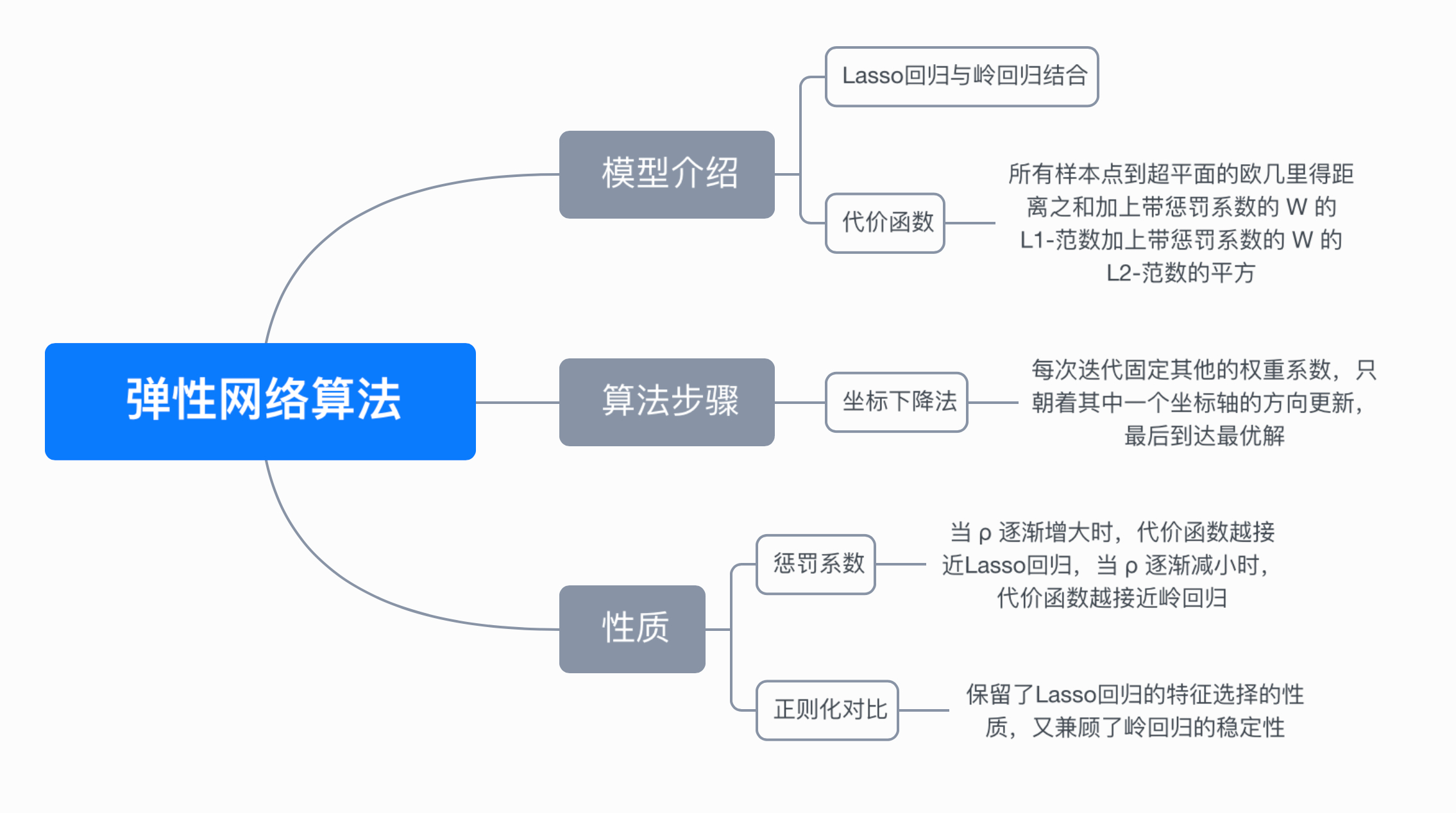
七、思维导图

完整演示请点击这里