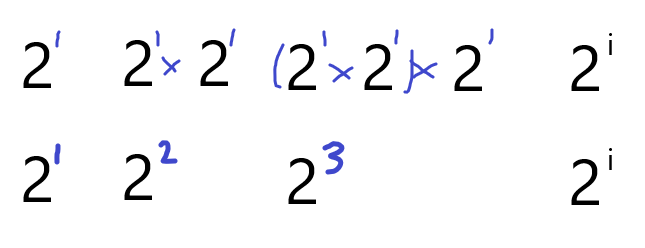Java教程
算法—算法的时间空间复杂度
本文主要是介绍算法—算法的时间空间复杂度,对大家解决编程问题具有一定的参考价值,需要的程序猿们随着小编来一起学习吧!
1. 事后分析法
缺点:不同的数据规模,不同的机器下算法运行的时间不同,无法做到计算运行时间
2. 事前分析法
2.1 大O时间复杂度
渐进时间复杂度 随着n的增长,程序运行时间跟随n变化的趋势
2.1.1 几个原则
去掉常数项
2(n^2) =n^2
一段代码取时间复杂度最高的
test(n) {
//时间复杂度n^3
for(int i = 0; i < n ; i++){
for(int i = 0; i < n ; i++){
for(int i = 0; i < n ; i++){
print(n);
}
}
}
//时间复杂度n^2
for(int i = 0; i < n ; i++){
for(int i = 0; i < n ; i++){
print(n);
}
}
//时间复杂度n
for(int i = 0; i < n ; i++){
print(n);
}
}
这段代码的时间复杂度为n3+n2+n
当n足够大时,n2和n与n3相比太小,可以忽略不计
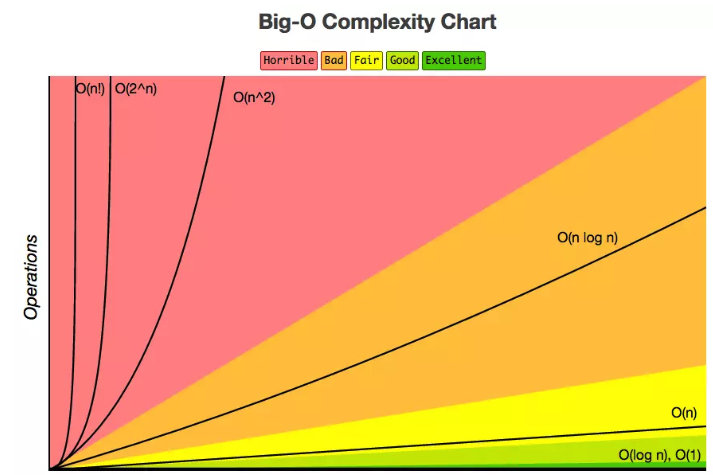
2.1.2 常见复杂度
o(1)
i = i + 1;
o(n)
test(n){
for(int i = 0 ;i < n;i++){
print(i);
}
}
o(n^2)
test(n){
for(int i = 0 ;i < n;i++){
print(i);
for(int j = 0 ;j < n;j++){
print(i);
}
}
}
o(log2n)
PS:如果ax =N(a>0,且a≠1),那么数x叫做以a为底N的对数,记作x=logaN,读作以a为底N的,其中a叫做对数的底数,N叫做真数。
test(n) {
int i = 1;
while (i <= n) {
i = 2 * i;
}
}
随着循环次数的增加,i的值变化如下
根据对数函数的公式 2的i次方等于n,i等于log2n
2.2 最好情况时间复杂度
数据比较有序的情况的时间复杂度
2.3 最坏情况时间复杂度
数据完全无序
3. 空间复杂度
与n无关的代码空间复杂度可以忽略
空间复杂度O(n)
test(n) {
//在内存中开辟了一个长度为n的数组
List array = List(n);
print(array.length);
}
这篇关于算法—算法的时间空间复杂度的文章就介绍到这儿,希望我们推荐的文章对大家有所帮助,也希望大家多多支持为之网!
您可能喜欢
-
百万架构师第十三课:源码分析:Spring 源码分析:Spring核心IOC容器及依赖注入原理|JavaGuide01-10
-
便捷好用的电商API工具合集01-10
-
必试!帮 J 人团队解决物流错发漏发的软件神器!01-09
-
不容小觑!助力 J 人物流客服安抚情绪的软件!01-09
-
为什么医疗团队协作离不开智能文档工具?01-09
-
惊叹:J 人团队用啥软件让物流服务快又准?01-09
-
如何利用数据分析工具优化项目资源分配?4种工具推荐01-09
-
多学科协作难?这款文档工具可以帮你省心省力01-09
-
团队中的技术项目经理TPM:工作内容与资源优化策略01-09
-
JIT生产管理法:优化流程,提升竞争力的秘诀01-09
-
2024全球互联网流量分析报告01-09
-
如何提升学校行政管理中的进度追踪效率?4个实用策略和3款工具推荐01-09
-
提升直播效果的复盘技巧,你必须知道的五个步骤01-09
-
电商蛇年营销实战:看板工具提升效率效果01-09
-
产品开发中如何解决跨团队协作问题?协同工具来解决这些问题01-09
栏目导航