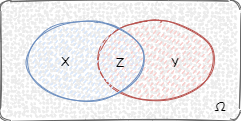
# 概率相关 ## 从骰子实验引出的各种概率概念 1.投骰子，出现点数为 6 的概率 $\frac{1}{6}$. 投骰子，**已知出现点数为偶数**，出现点数为 6 的概率则是 $\frac{1}{3}$，这个概率即 **条件概率**。 2.**条件概率**为：假设我们知道 A 事件已经发生，在此基础上我们想知道 B 事件发生的概率，这个概率为条件概率，记作 $P(B|A)$ 3.**古典概率模型**：假设一个实验，有 **$\Omega$ 个等可能性的结果**，事件 A 包含其中 $X$ 个结果，事件 B 包含其中 $Y$ 个结果，$Z$ 代表其中交叉的事件：  事件 A 发生的概率：$P(A) = \frac{X}{\Omega}$；事件 B 发生的概率：$P(B) = \frac{Y}{\Omega}$；事件 A、B 都发生的概率：$P(AB) = \frac{Z}{\Omega}$如果事件 A 已经发生，那么事件 B 也发生的概率是 $P(B|A) = \frac{Z}{X}$，将公式展开： 这个公式就是条件概率公式 $$ P(B|A) = \frac{\frac{Z}{\Omega}}{\frac{X}{\Omega}}= \frac{P(AB)}{P(A)} $$ 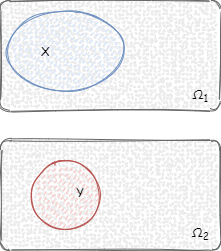4.如果条件概率 $P(B|A)$ 大于 $P(B)$，代表事件 A 的发生会促进事件 B 的发生，例如上面投骰子的例子。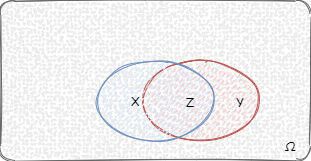还有可以看下图，本身 $P(B)$ 的概率是比较小的，在事件 A 已发生的情况下，由于相交部分较多，事件 B 发生的概率也提升了：  5.如果条件概率 $P(B|A)$ 小于 $P(B)$，代表事件 A 不会促进事件 B 的发生，例如事件 A 为投骰子点数为偶数，事件 B 为投骰子点数小于 < 4，事件 A 和 事件 B 发生的概率都为 $1/2$，事件 A、B 同时发生的概率是 $1/6$，条件概率 $P(B|A)$ 为 $1/3$。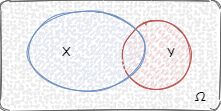还有可以看下图，本身 $P(B)$ 的概率是比较大的，在事件 A 已发生的情况下，由于相交部分较少，事件 B 发生的概率被降低了：  6.如果条件概率 $P(B|A)$ 等于 0，代表事件 A 与事件 B 完全不相交，即事件 A 发生则事件 B 一定不会发生，事件 A 与事件 B 是**不相容事件**，或者是**互斥事件**。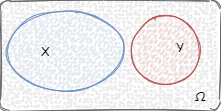如下图所示：  7.还有可能条件概率 $P(B|A)$ 等于 $P(B)$，在这种情况下其实就是事件 A、B 的发生互不相关，例如有两个骰子，事件 A 为骰子 1 投出点数 6，事件 B 为骰子 2 投出点数 2，事件 A 和 事件 B 发生的概率都为 $1/6$，那么事件 A、B 同时发生的概率是 $\frac{1}{36}$，条件概率 $P(B|A)$ 等于 $\frac{1}{6}$，我们一般称这种为独立事件。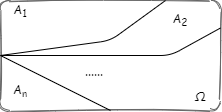如下图所示：  ## 全概率公式与骰子实验验证 假设有 $A_1,A_2,...,A_n$ 这些互斥事件，包含了实验所有可能的结果：  即有$P(A_1) + P(A_2) + ... + P(A_n) = 1$。拿刚刚的骰子举例，其实就是抛一次骰子，点数分别为 1，2，3，4，5，6. 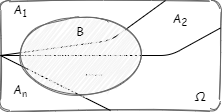假设再有一个事件 B，用古典概率表示如图：  事件 B 的概率，可以通过事件 B 在 $A_1,A_2,...,A_n$ 这些互斥事件上的条件概率以及这些事件的概率进行计算，即全概率公式： $$ 条件：P(A_1) + P(A_2) + ... + P(A_n) = 1 $$ $$ 结果：P(B) = P(B\Omega) = P(BA_1) + P(BA_2) + ... + P(BA_n) = P(A_1)P(B|A_1) + P(A_2)P(B|A_2) + ... + P(A_n)P(B|A_n) $$ 例如事件 B 就是投出的骰子为偶数，$P(B) = \frac{1}{2}$，$P(A_{点数=1})P(B|A_{点数=1}) + P(A_{点数=2})P(B|A_{点数=2}) + P(A_{点数=3})P(B|A_{点数=3}) + P(A_{点数=4})P(B|A_{点数=4}) + P(A_{点数=5})P(B|A_{点数=5}) + P(A_{点数=6})P(B|A_{点数=6}) = \frac{1}{6} * 0 + \frac{1}{6} * 1 + \frac{1}{6} * 0 + \frac{1}{6} * 1 + \frac{1}{6} * 0 + \frac{1}{6} * 1 = \frac{1}{2}$ ## 全概率公式的使用：足球预测 全概率公式的意义在于：在大多数情况下，我们是**很难像骰子实验一样直接得出事件 B 的概率**的，我们需要限定事件的样本空间，根据现有样本抽象出事件 $A_1,A_2,...,A_n$，同时统计这些事件上 B 发生的概率，最后得出事件 B 的概率。 举个例子即推测本次欧洲杯英国队对阵德国队，英国队胜利的概率，我们可以通过历史比赛数据（例如近几届欧洲杯比赛数据，以及两队对阵比赛数据）估算出英国队进球数为 0，1，2，3，4，5... 的概率，德国队进球数为 0，1，2，3，4，5... 的概率，其中**英国队进球数大于德国队即英国队胜利的概率**。这就是全概率公式的一种应用。 ## 由因推果与由果推因 全概率公式就是**由因推果**，一个典型的例子就是上面提到本次欧洲杯英国队对阵德国队，英国队胜利的概率的推测。我们根据以往比赛数据，可以算出英国队还有德国队的平均进球，进球概率一般符合**泊松分布**（这个我们之后还会提到，还会用这个例子详细分析），根据**泊松分布**，我们可以可以得出英国队还有德国队进球数 n 的概率，假设英国队平均进球为 1.67，德国队平均进球为 1.52 则（我们这里只考虑到进球数为 4 的情况）： 球队 | 进球数为 0 | 进球数为 1 | 进球数为 2 | 进球数为 3 | 进球数为4 | ---|---|---|---|---|---| 英国队 | 0.1882 | 0.3144 | 0.2625 | 0.1461 | 0.061 | 德国队 | 0.2187 | 0.3324 | 0.2527 | 0.128 | 0.0486 | 假设 $P(A_0)$ 为英国队进球数为 0 的概率并以此类推： $$ P(A_0) = 0.1882 $$ $$ P(A_1) = 0.3144 $$ $$ P(A_2) = 0.2625 $$ $$ P(A_3) = 0.1461 $$ $$ P(A_4) = 0.061 $$ 假设 $P(B)$ 为英国队胜利的概率，则根据全概率公式有： $$ P(B) = P(A_0)P(B|A_0) + P(A_1)P(B|A_1) + P(A_2)P(B|A_2) + P(A_3)P(B|A_3) + P(A_4)P(B|A_4) $$ $$ P(B|A_0) = 0 $$ $$ P(B|A_1) = 德国队进球为 0 的概率 = 0.2187 $$ $$ P(B|A_2) = 德国队进球为 0，1 的概率 = 0.2187 + 0.3324 = 0.5511 $$ $$ P(B|A_3) = 德国队进球为 0，1，2 的概率 = 0.2187 + 0.3324 + 0.2527 = 0.8038 $$ $$ P(B|A_4) = 德国队进球为 0，1，2，3 的概率 = 0.2187 + 0.3324 + 0.2527 + 0.128 = 0.9318 $$ $$ P(B) = 0.1882 * 0  +  0.3144 * 0.2187 + 0.2625 * 0.5511 + 0.1461 * 0.8038 + 0.061 * 0.9318 = 0.3877 $$ 但是，现实问题中，我们经常还会遇到由果推因的问题，例如我们体检，检测出来了胆囊息肉，那它究竟是否是肿瘤形成的还是胆固醇形成的或者是其他原因呢？这就需要我们从这个结果推测形成的原因。这就引出了**贝叶斯公式** ## 从足球预测例子理解先验概率与后验概率 在提到贝叶斯公式之前，我们先搞清楚两个概念，**先验概率**与**后验概率**。 **先验概率**一般是通过经验得出，即根据历史采集到的数据，没有做任何限制，得出的经验概率。上面的例子提到的通过历史比赛数据推测出来的两队进球数的概率，就是**先验概率**。这时候假设比赛开始，然后发生了一个事件，德国队后卫失误被英国队凯恩先进了一球，这时候我们需要在这个前提下重新计算两队进球数的概率，这个就是**后验概率**。 **先验概率**即完全根据历史数据推测出的经验概率，没有任何已发生前提情况下的概率。**后验概率**即观察到某个现象需要对**先验概率**进行修正的概率。可以这样简单理解，比赛开始前，估计的概率一般就是先验概率，比赛开始后，发生红黄牌，点球，进球，换人等等这些事件后，对概率进行修正后得出的就是后验概率。 ## 贝叶斯公式与胆囊息肉形成原因推测 假设有事件 A、B，则： $$ P(A|B) = \frac{P(AB)}{P(B)} = \frac{P(B|A)P(A)}{P(B)} $$ 这就是贝叶斯公式，我们再结合起来全概率公式，假设我们事件 $A_1, A_2, ..., A_n$ 这些互斥事件构成了样本空间的全集，则有： $$ P(A_1|B) = \frac{P(B|A_1)P(A_1)}{P(B)} = \frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1) + P(B|A_2)P(A_2) + ... + P(B|A_n)P(A_n)} $$ 我们来用胆囊息肉形成原因推测举个例子，假设我们统计到在某个医院一百万个病人样本中，患有肿瘤的有 8%，其中的 20% 曾经发现胆囊息肉，具有高胆固醇症状的人有 80%，其中 40% 曾经发现胆囊息肉，剩下其他的 12% 中 30% 曾经发现胆囊息肉。假设 $A_1$ 为患有肿瘤，$A_2$ 为胆固醇，$A_3$ 为其他。$B$ 为胆囊息肉。则胆囊息肉为肿瘤的概率为： $$ P(A_1|B) = \frac{P(B|A_1)P(A_1)}{P(B|A_1)P(A_1) + P(B|A_2)P(A_2) + P(B|A_3)P(A_3)} = \frac{0.2 * 0.08}{0.2 * 0.08 + 0.4 * 0.8 + 0.3 * 0.12} = 0.043 $$