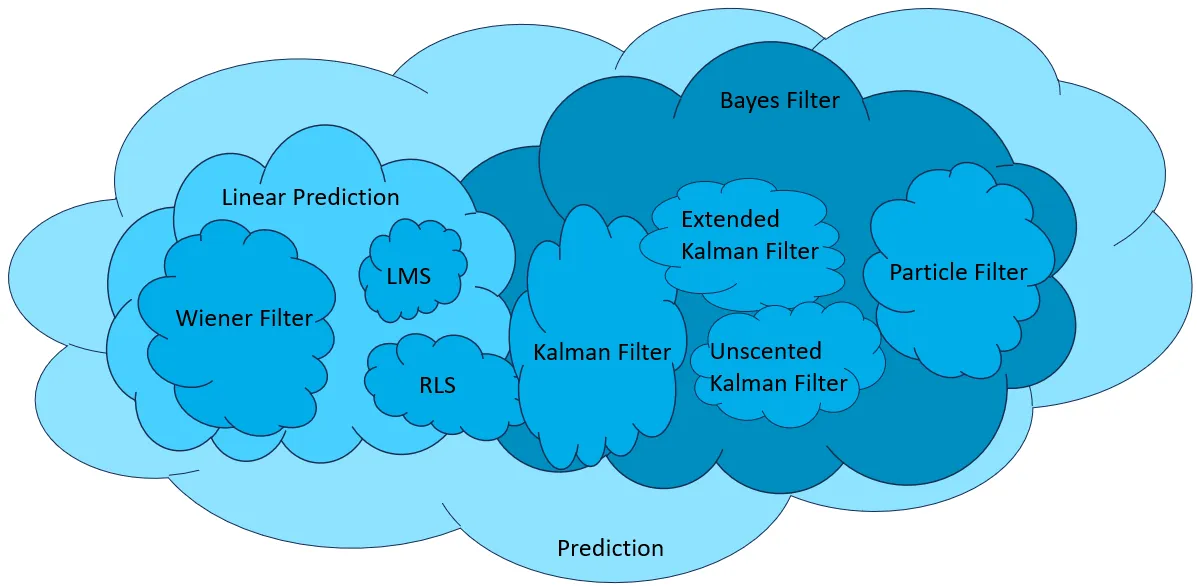
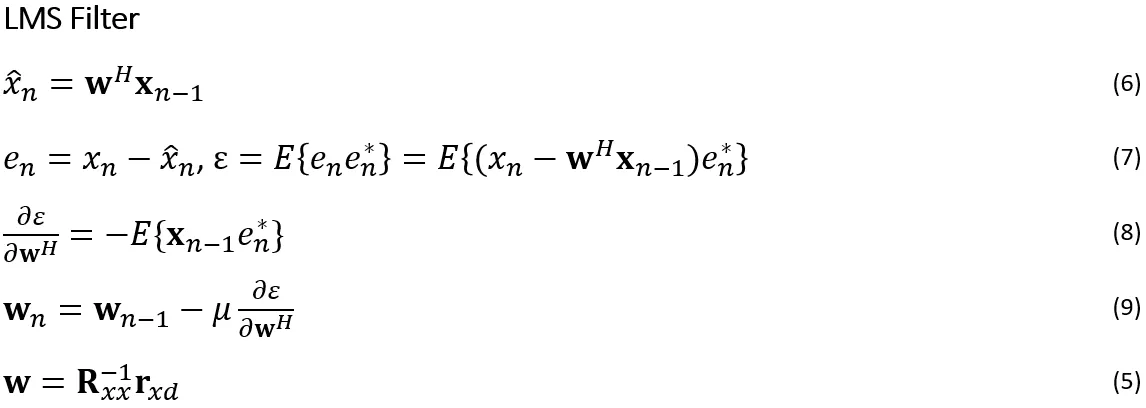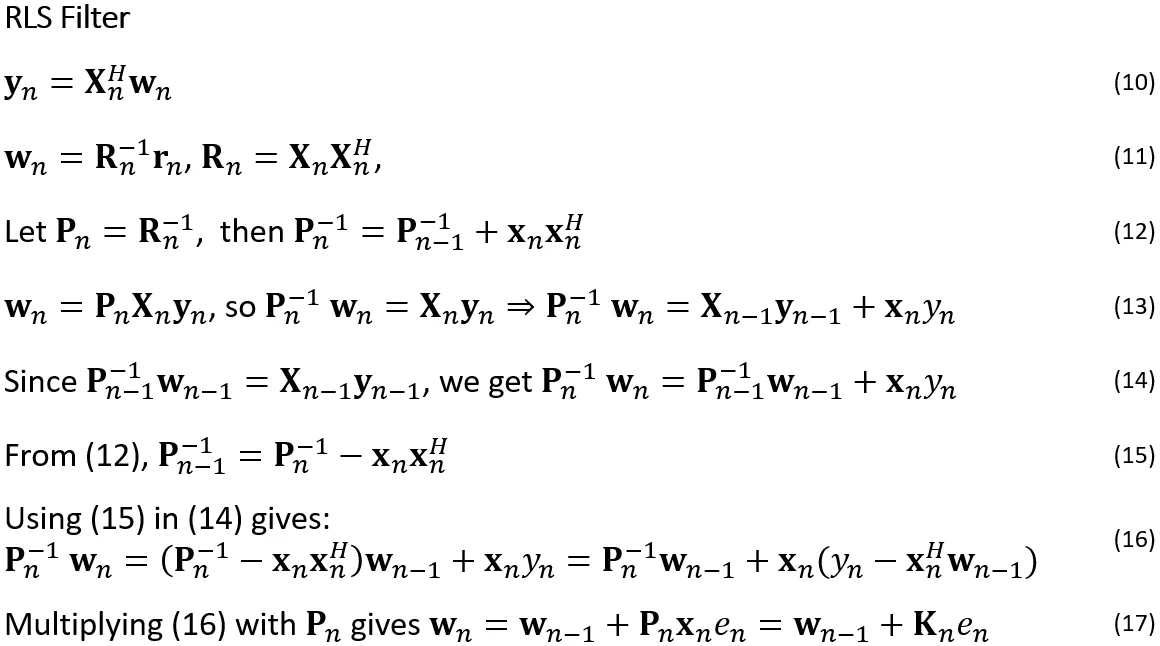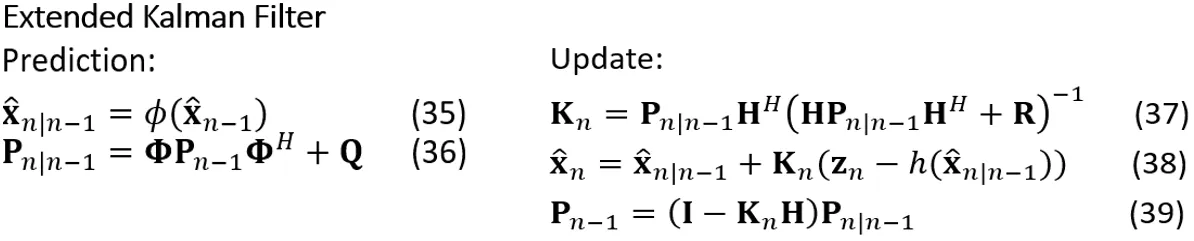人工智能学习
预测的艺术:预AI时代的滤波技术讲解
给定一个过去样本序列,这些样本收集在向量 x 中,下一个样本可以预测为之前样本的加权组合,y = x w。这里的 表示共轭转置操作(就像通常使用的上标 H 一样),所有粗体小写字母都是列向量,斜体小写字母是标量,粗体大写字母是矩阵。这是相当标准的记号,我希望亲爱的读者在阅读本文时能记住这一点。为了提供额外的见解,展示的方程以图像形式分组,可以被随意读者忽略。我的目标是传达关键思想和直觉,而不是严格证明它们。交代清楚之后,让我们继续吧!
现在的问题是,我们如何选择权重?如果我们估计 y 为 x w ,而期望的输出是 d,则均方误差是 E{|d-y |²},其中 E{…} 是期望算子,由于 y 和 d 是随机变量。用 y = x w 来计算,我们可以得到如图所示的均方误差方程 2。展开这个方程(方程 3),计算关于 w 的偏导数(方程 4),并将其设为零,这样我们就能得到使均方误差最小的权重 w (方程 5)。最优权重的解取决于 x 的协方差矩阵,以及 x 和 d 之间的互协方差。
顺便说一下,对 w 的导数是矩阵微积分中的一个巧妙技巧,因为它避免了在计算 d(Ax)/dx 时出现的烦人的转置,即 d(Ax)/dx 等于 A 的转置。另外需要注意的是,在对 w 求导时,变量 w 被视为常量。直观地说,导数量化了一个函数在其中一个变量有微小变化时的变化量。一个变量与其复共轭相隔很远,因此不会影响函数的局部变化。
给定输入向量 x[n-1] 中收集的序列 x[n -1], …, x[n-N],在时刻 n 的样本 x[n] 可以通过维纳滤波器计算得出。我们可以将所有这些 x[n -1],x[n -2],…,x[n-M] 向量组合成一个 N x M 的矩阵 X。然后我们有线性系统 y = X w。两边乘以 X 就可以得到 Xy = XX w,再乘以 XX 的逆矩阵就可以得到 w = inverse(XX )Xy,这就是最小二乘法的解。我们可以看出矩阵 XX 是样本协方差矩阵(假设矩阵 X 的列已经被零均值化),而 Xy 是样本交叉协方差向量。
因此,这种线性预测需要计算协方差矩阵,如果我们不想让预测偏离轨道,协方差矩阵需要对每个新样本进行更新。这意味着需要对两个 N x M 的矩阵进行相乘,然后计算矩阵的逆。我们能否迭代更新权重呢?这时引入了 LMS 滤波器。
LMS滤波器利用梯度下降法来调整权重。因为这是一个线性系统(参见方程6),均方误差(参见方程7)是一个凸函数,所以可以利用梯度(参见方程8)来调整权重(参见方程9)。沿着与梯度相反的方向移动可以最小化误差。想象在一个抛物线上——为了达到最低点,你需要沿着斜率的相反方向移动。梯度通过LMS步长调整,收敛性取决于所选的步长。我们还可以进一步讨论步长和收敛性,归一化输入(NLMS)能获得更好的数值稳定性,但这对当前讨论来说并不重要。
另一种迭代更新权重的方法是通过观察最小二乘解,看看是否可以递归地计算协方差矩阵,从而得到递归最小二乘(RLS)滤波器。以下方程显示了一些巧妙的技巧,使我们能够做到这一点。这里的数学并不复杂(仅仅是代入操作),只需您耐心地跟着这些方程,细心一些即可。如果看起来太复杂,关键是权重可以根据误差乘以一个“增益”来更新,这个增益取决于递归计算出的逆协方差矩阵。
我们快速地过一遍RLS滤波器的方程。我们从系统模型(方程10)和使用样本协方差矩阵的维纳解(方程11)开始。样本协方差矩阵可以很容易地在每次我们有一个新样本时更新——我们只需构建向量x[n],计算外积x[n]x *[n]并将其加到之前的协方差矩阵上(尽管是平均的,但这里为了简化推导过程忽略了这一点)。这里的巧妙之处在于定义逆协方差矩阵P(方程12)并用P重新表述维纳解(方程13),其中我们利用样本交叉协方差也可以像样本协方差一样更新。方程13中时间_n_的情况同样适用于时间n-1的情况,利用这一点可以得到方程14。进行一些替换(方程15、16)后,得到最终的表达式(方程17),我们看到权重是通过使用依赖于逆协方差矩阵P的增益K来缩放误差而更新的。可以使用矩阵求逆引理推导出逆协方差矩阵的递归更新方程,但这里我们省略了这一点。
让我们来回顾一下我们到现在为止看到的内容。线性预测可以通过维纳滤波器实现,其中滤波器权重依赖于协方差矩阵。我们可以通过梯度下降递归地更新这些权重,这将给我们一个LMS滤波器,该滤波器使用步长来缩放梯度。使用RLS滤波器可以提供额外的见解,即权重可以通过用依赖于逆协方差矩阵的增益来缩放误差进行更新。
虽然 LMS 和 RLS 滤波器算法可以用来迭代更新线性预测器的权重,但另一种完全不同的方法是找到一个系统的状态 x[n],使得在给定当前和过去测量值的情况下,x[n] 的似然概率最大。这个状态 x[n] 将包含所有当前和过去测量的信息,就像深度神经网络中的隐藏层那样,或者像循环神经网络语言模型中的思想向量。然后可以用该状态 x[n] 来预测观测值 z[n]。简而言之,我们要找的是具有最高条件概率 p(x[n] | z[n], z[n -1], …) 的 x[n]。涉及条件概率时,可以使用贝叶斯规则:p(A|B) = p(B|A)p(A)/p(B)。
贝叶斯法则给出了方程18,其中第一个乘积项(方程19)可以简化,因为系统状态x[n]预计包含了所有过去测量的所有信息,因此不需要对过去测量进行条件化。第二个乘积项(方程20)可以通过引入系统先前的状态x[n-1]并对其积分求解,写成边缘概率密度函数。方程18中的分母与x[n]无关,因此可以当作归一化因子处理。我们可以将方程19和方程20结合,得到方程21的表达式,其中当前状态的概率是基于先前状态的概率和状态转移概率的预测。然后根据观察值来更新当前状态的概率。
因此,贝叶斯滤波允许递归预测可能性,然后根据测量概率更新预测的可能性值。关键在于每个迭代的预测和更新步骤。现在我们已经为引入卡尔曼滤波器做好了准备。
此时,敏锐的读者可能就会想问,为什么还要费心创建状态向量,既然线性预测器通过迭代更新权重已经做得很好了。一个原因是线性预测器只能基于过去的值进行预测,并且无法考虑任何额外的控制输入。比如在机器人导航中,下一个位置不仅依赖于上一个位置,还依赖于控制输入,例如,控制机器人移动或停止。
在这里省略了控制输入部分,从而简化了方程,并专注于基于过去观测的预测问题。但是,具有相关状态的递归贝叶斯滤波器框架能够应对更复杂的系统。
给定一个将状态 x[n] 映射到观测值 z[n] 的线性观测模型,以及一个根据当前状态 x[n] 预测下一个状态 x[n+1] 的线性状态演化模型,卡尔曼滤波器允许在每个时间点 n 迭代预测和校正状态 x[n]。预测步骤依赖于状态演化模型,而校正步骤则根据实际测量和预测观测值之间的误差(通过观测模型从预测的状态得出)来更新状态。在误差被用于更新状态之前,会被卡尔曼增益加权。卡尔曼增益是使得误差协方差最小的最优增益。误差协方差矩阵也会根据卡尔曼增益迭代更新。
卡尔曼滤波器使用的方程如下面的图片所示。对于那些之前从未见过这些方程的人而言,线性模型仅仅是矩阵。这种奇怪的下标 n|n-1 表示在时间 n 的量是根据时间 n-1 的先前估计预测出来的。它将预测与修正/更新步骤后的最终估计区分开来。如果有助于理解,可以将标有 n|n-1 的量视为在当前测量值校正之前的中间预测值。
但是这些预测公式和更新公式是从哪里来的?给定前一状态的估计值,公式24是直接使用状态演化模型进行预测。公式25中的预测误差协方差矩阵也可以通过状态演化模型计算得出。公式27是基于误差对预测进行修正,修正的权重根据卡尔曼增益来调整。回想一下,这与我们在RLS滤波器中所做的操作相同,只是卡尔曼增益的计算方式不同。此外,公式27可以重新排列为x[n] = (I - KH)x[n|n-1] + Kz[n],当H为单位矩阵(意味着状态与观测一致时),公式变为x[n] = (I - K)x[n|n-1] + Kz[n]。这可以理解为新估计是前一估计和当前测量的加权平均。当前测量的权重取决于卡尔曼增益,而卡尔曼增益则是由过程噪声协方差和测量噪声协方差共同决定的。
为了理解卡尔曼增益是如何得出的,请参见下方的方程式。通过使用最终估计(方程30)和预测误差协方差,可以将实际状态和估计状态之间的误差协方差(方程29)扩展为方程33中的表达式,即方程33。然后通过最小化误差协方差矩阵的迹来求得卡尔曼增益。
需要注意的是,这种公式要灵活得多。由于它的递归特性,我们可以让预测依赖于更多的历史样本而不需要增加权重的数量,就像IIR滤波器对比FIR滤波器一样。该模型可以包含不同类型的实际物理量(例如:距离、速度、角度),然后将它们组合在一起,而使用线性预测器则做不到这一点。
卡尔曼滤波器是一种线性最小均方滤波器,在所有涉及的随机变量均为高斯分布(也称为正态分布)时,它是最优的线性滤波器。值得注意的是,高斯分布完全由前两个统计量(均值和协方差)确定。并且,任何高斯分布随机变量的线性变换仍然是高斯分布。这使得卡尔曼滤波器能够在每个时间步使用最优的MMSE增益来更新协方差矩阵,以跟踪高斯随机过程的变化。
如果分布不是高斯分布,在这种情况下,卡尔曼滤波器就不再是最优的选择了,因为它只根据均值和协方差来工作。估计的随机过程将按照非高斯分布的高斯近似值来估算。
请注意,如果卡尔曼滤波器所用的系统模型不是线性的,高斯分布特性在变换过程中不会被保留。在这种非线性情况下,卡尔曼滤波器也会失去其最优性特性。
卡尔曼滤波器框架的多样性和实用性使其在系统模型非线性、不再是最优的情况下仍然可以考虑使用。即使我们接受它可能不是最优的这一点,我们应该如何应用卡尔曼滤波方程呢?因为这些方程使用矩阵计算,所以需要一个线性模型。
如下面的图片所示,我们可以通过只保留前两项来使用泰勒展开将非线性函数线性化。因为协方差矩阵的演变仅仅依赖于雅可比矩阵(即一阶偏导数的矩阵),卡尔曼滤波方程基本上保持不变。
预测扩展卡尔曼滤波器的预测和校正公式如下图所示。请注意以下几点:只有状态演变(方程35)和预测误差计算(方程38)与线性模型的卡尔曼滤波方程相比有所变化。
让我们再回顾一下。使用魏纳滤波器的线性预测使用依赖于逆协方差矩阵的权值。这些权值可以使用LMS(梯度下降法)或RLS(递归最小二乘法)迭代更新。在RLS中,逆协方差矩阵递归计算,用于加权误差的增益因子也依赖于逆协方差矩阵。由于这是一FIR滤波器,如果我们增加过去的观测数量,滤波器的长度也会增加。
贝叶斯滤波提供了一种递归估计下一个状态的另一种框架。这一过程可以分为两个步骤:首先,基于之前的估计进行预测;然后,通过实际测量来修正预测,最终得到当前的估计。
卡尔曼滤波器是一种线性滤波器,在随机过程呈高斯分布且所用模型为线性时最为有效。若模型是非线性的,需要使用基于泰勒级数近似的的方法对其进行线性化,以便可以在卡尔曼滤波框架中应用线性方程。
卡尔曼滤波的一个关键步骤是递归计算误差协方差矩阵,这是为了计算卡尔曼增益。这个计算需要一个线性模型。如果我们不再进行递归估计,而是直接计算样本协方差会如何?这只需要一组样本,这些样本需要在均值周围有足够的分散,这样一组样本就可以用于计算样本协方差。
如果我们选取这样一套过去的状态向量样本,可以将其输入非线性函数来获取变换后的样本,并从这些样本中估计协方差。这种方法就叫做无迹卡尔曼滤波器。关于如何选择这些样本的详细信息,您可以在论文无迹卡尔曼滤波器的非线性估计中找到。此外,在YouTube上还有关于这一主题的精彩讲座(SLAM课程第六部分):SLAM课程 — 06 — 无迹卡尔曼滤波器。
请注意,卡尔曼滤波框架仍然仅使用均值和协方差,因此其估计值仍然是非高斯分布的高斯近似随机过程。
为什么还要接近高斯分布呢?如果我们保留许多样本(粒子),每个粒子代表系统的一种可能的状态,我们就可以使用非线性函数来演化这些可能的状态。当我们有测量值时,根据预测值与实际测量值的接近程度来更新每个粒子的重要性(权重)。重要性低的粒子将被剔除。这就是粒子滤波器的运作方式——这里不需要计算误差协方差矩阵或增益。因此,这种方法并不限制我们使用高斯分布的形式。
这就结束了这篇撰写。当我提到我打算写这篇文章时,一位好朋友向我推荐了《卡尔曼滤波最简单教程》(The Easiest Tutorial on Kalman Filter)。虽然该教程确实对它的目标读者很有帮助,但我更希望涵盖更多类型的预测滤波器,并展示它们之间的联系。如果你们觉得我达到了这个目标,那么我相信我的付出是值得的。如果你们确实这么认为,我会非常感激你们花时间在这里的评论区或领英上告诉我。
-
如何利用AI看板工具提升团队协作效率?10大深度评测与实用技巧01-04
-
带有自反功能的自适应检索增强生成系统01-03
-
FAISS向量数据库在生产LLM应用中的使用指南01-03
-
掌握RAG:深入探讨文本分割技巧01-03
-
深入探究结构化输出的应用技巧01-03
-
因果推断的基本问题:现代视角下的统计挑战01-03
-
OpenAI 新模型“草莓”来袭,o1-preview版本抢先看!01-03
-
利用知识图谱和大模型提升元数据管理的思考与实践(上篇)01-03
-
llama 3.1 — 技术规格和代码解析01-03
-
基于LangGraph的多代理应用开发利器01-03
-
打造自定义AI智维助手:基于Jira的自动化任务处理系统01-03
-
AI元年2024:全球人工智能大事件概览01-02
-
2024年20款热门好用AI工具,助力创作与工作管理01-02
-
揭秘:Fluss 与数据湖Paimon深度解析(一)01-02
-
效率革命:AI工具助力团队沟通12-31