物理中的强化学习：常微分方程与超参数调节

本文主要是介绍物理中的强化学习：常微分方程与超参数调节，对大家解决编程问题具有一定的参考价值，需要的程序猿们随着小编来一起学习吧！

使用gymnasium来控制微分方程并优化算法超参数

感谢 Brice Cooper 拍摄，图片来自 Unsplash

正如我们之前讨论的，强化学习（RL）为解决控制非线性物理系统的问题提供了一种强大的新工具。非线性物理系统的特点是复杂的行为，其中输入的小变化可能导致输出的显著变化，或者即使大输入变化也只导致小输出变化。解可能分裂，即相同的条件可能产生不同的结果，甚至可能具有路径依赖性，就像有“记忆”一样。我们介绍了两种将RL应用于非线性物理系统的方法：传统的基于神经网络的软演员评论家（SAC）算法，以及不常见的基于遗传算法的遗传编程（GP）算法，这种方法较少使用。

简而言之，SAC 使用两个神经网络，一个用于学习环境的行为方式，另一个用于确定最优策略。随着模型训练的进行，这些网络会不断更新，“评判网络”通过评估环境来帮助改善决定策略的“行动网络”。GP（遗传算法）基于生成一系列随机数学方程组成的“森林”，评估这些方程在环境中的表现情况，然后通过变异、组合或生成新的随机方程来优化性能。当应用于gymnasium的摆的经典控制环境时（如摆的经典控制），GP 方法显示出更快的收敛。现在我们继续扩展该研究，（1）引入基于常微分方程的更复杂的物理系统，（2）探索超参数调整对 SAC 和 GP 算法性能的可能影响。

关于常微分方程（ODEs）的工作

物理系统通常可以通过微分方程或包含导数的方程来建模。力也因此可以表示为导数，牛顿定律亦是如此，麦克斯韦方程亦是如此，因此微分方程可以描述大多数物理问题。微分方程描述了系统如何根据当前状态变化，实际上定义了状态的转换。微分方程组也可以写成矩阵或向量的形式。

其中 x 是状态向量，A 是由物理动力学决定的状态转移矩阵，而 x 的导数（或 dx/dt）是状态随时间变化的变化。本质上，矩阵 A 对状态 x 进行操作，使其随时间向前推进一小步。这种模型通常用于线性方程（其中 A 的元素不包含任何状态向量），但也可以用于非线性方程，其中 A 的元素可能包含状态向量，这可能导致上述提到的复杂行为。该方程描述了环境或系统如何随时间发展，从特定初始条件出发。在数学上，这些被称为初始值问题，因为评估系统如何发展需要指定一个初始状态。

上述表达描述了一类特定的常微分方程（ODE），其中导数都是关于一个变量的，通常是时间，但偶尔也可能是空间。点表示 dx/dt，或随着时间增量变化的状态变化。ODE 研究得很透彻，线性系统中的 ODE 有许多可用的解析解法。解析解允许解用变量表达，从而使整个系统更便于分析。非线性系统的解析解法较少，但某些类型仍有可用的解析解。不过，大多数情况下，非线性（或某些线性）ODE 更适合通过数值模拟求解，即在每个时间步长上计算数值解。

模拟围绕着找到微分方程的近似解，通常是通过有限差分法，这种近似在小的时间范围内具有已知的准确性。计算机可以通过处理许多小的时间步长来展示系统的发展。有许多可用的算法来进行此类计算，例如 Matlab 的 ODE45 或 Python SciPy 的 solve_ivp 函数。这些算法接受一个常微分方程和一个初始条件（初值问题），自动确定最优步长，并推进到指定的结束时间点。

如果我们能对一个常微分方程系统施加正确的控制输入，我们通常可以将其驱动到所需的状态。正如我们上次讨论的那样，强化学习提供了一种确定非线性系统正确输入的方法。为了开发强化学习，我们将再次使用gymnasium环境，但这次我们将基于我们自己的常微分方程创建一个自定义的gymnasium环境。遵循Gymnasium文档，我们创建一个将涵盖状态空间的观察空间，以及用于控制空间的动作空间。我们初始化/重置gymnasium环境到状态空间中的任意一点（但需要注意，并非所有期望的最终状态都可以从任意初始状态到达）。在gymnasium的step函数中，solve_ivp调用一个函数，该函数包含我们正在处理的具体常微分方程，在应用控制K的短时间步长内解决该方程的动态。solve_ivp调用函数以解决具有控制K的常微分方程在短时间步长内的动态。代码可在[git](https://github.com/retter-berkeley/PhysicsGyms)上查阅。init为系统中的每个状态创建一个观察空间，而reset则随机设定每个变量的起点，确保这些点离原点有最小距离。在step函数中，solve_ivp调用函数解决具有控制K的常微分方程在短时间步长内的动态。

    #来自https://www.gymlibrary.dev/content/environment_creation/  
    #为Moore-Greitzer模型创建gym环境  
    #动作空间：连续浮点数，范围在±10.0（可选缩放至μ）  
    #观察空间：-30,30 x2 浮点数，表示x,y,z  
    #奖励：-1*(x^2+y^2+z^2)^1/2（尽量将状态驱动到0）  

    #Moore-Grietzer模型：  

    from os import path  
    from typing import Optional  

    import numpy as np  
    import math  

    import scipy  
    from scipy.integrate import solve_ivp  

    import gymnasium as gym  
    from gymnasium import spaces  
    from gymnasium.envs.classic_control import utils  
    from gymnasium.error import DependencyNotInstalled  
    import dynamics  #包含solve_ivp公式的本地库  
    from dynamics import MGM  

    class MGMEnv(gym.Env):  #无渲染模式
        def __init__(self, render_mode=None, size=30):  

            self.observation_space =spaces.Box(low=-size+1, high=size-1, shape=(2,), dtype=float)  

            self.action_space = spaces.Box(-10, 10, shape=(1,), dtype=float)   
            #需要将动作更新为正态分布  

        def _get_obs(self):  
            return self.state  

        def reset(self, seed: Optional[int] = None, options=None):  
            #需要下面的步骤来初始化self.np_random  
            super().reset(seed=seed)  

            #开始随机选取x1和x2的初始值  
            np.random.seed(seed)  
            x=np.random.uniform(-8.,8.)  
            while (x>-2.5 and x<2.5):  
                np.random.seed()  
                x=np.random.uniform(-8.,8.)  
            np.random.seed(seed)  
            y=np.random.uniform(-8.,8.)  
            while (y>-2.5 and y<2.5):  
                np.random.seed()  
                y=np.random.uniform(-8.,8.)  
            self.state = np.array([x,y])  
            observation = self._get_obs()  

            return observation, {}  

        def step(self,action):  

            u=action.item()  

            result=solve_ivp(MGM, (0, 0.05), self.state, args=[u])  

            x1=result.y[0,-1]  
            x2=result.y[1,-1]  
            self.state=np.array([x1.item(),x2.item()])  
            done=False  
            observation=self._get_obs()  
            info=x1  

            reward = -math.sqrt(x1.item()**2)#+x2.item()**2)  

            truncated = False #占位符，未来可用于限制发散的解决方案  
            info = x1  

            return observation, reward, done, truncated, {}

以下是Moore-Greitzer模式（MGM）函数的动力学。此实现基于solve_ivp的文档。设置了限制以避免解发散；如果系统达到限制，奖励将很低，以促使算法调整控制策略。根据这里提到的模板创建基于ODE的gymnasium应该是比较简单的：将观察空间的大小调整到与ODE系统的维度相匹配，并根据需要更新动力学方程。

    def MGM(t, A, K):  
        #非线性逼近气体涡轮发动机的进气/失速动态特性，根据Moore-Greitzer模型，  
        #出自"非线性系统的输出反馈控制使用控制收缩度量和凸优化"，  
        #作者Manchester和Slotine  
        #这是一个二维系统，x1代表质量流量，x2表示压差增量  
        x1, x2 = A  
        if x1 > 20:  x1 = 20.  
        else if x1 < -20:  x1 = -20.  
        if x2 > 20:  x2 = 20.  
        else if x2 < -20:  x2 = -20.  
        dx1 = -x2 - 1.5 * x1 ** 2 - 0.5 * x1 ** 3  
        dx2 = x1 + K  
        dx1 计算公式为：-x2 - 1.5 * x1 ** 2 - 0.5 * x1 ** 3  
        dx2 计算公式为：x1 + K  
        return np.array([dx1, dx2])

在这个例子中，我们使用基于Moore-Greitzer模型（MGM）的常微分方程来描述燃气涡轮发动机的喘振和失速动力学¹。该方程描述了发动机流量和压力之间的耦合阻尼振荡。控制器的目标是通过控制发动机的压力，迅速将振荡减小到零。MGM促进了非线性控制设计的重大进展，使其成为SAC和GP方法的有趣测试案例之一。描述该方程的代码可以在Github找到。另外还列出了三个其他的非线性常微分方程。Van der Pol振荡器是一个基于电子系统动力学的经典非线性振荡系统。Lorenz吸引子是看似简单的ODE系统，它可以产生混沌行为，或者对初始条件高度敏感。第三个是由Duriez/Brunton/Noack提供的平均场ODE系统，描述了稳定和不稳定波的复杂相互作用的发展，作为湍流流体流动的近似模型。

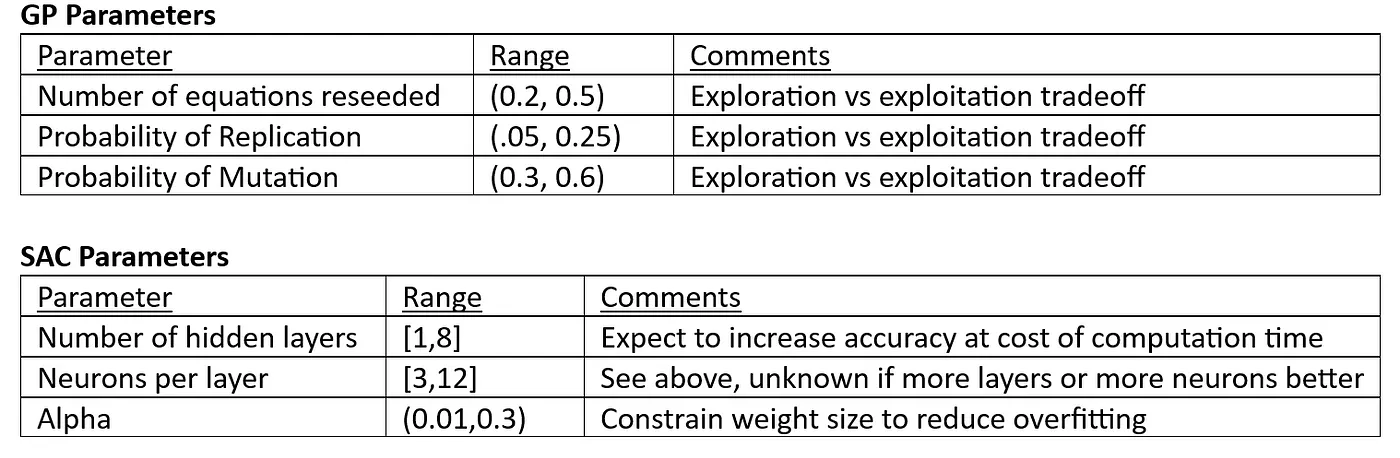
为了避免重复上文的分析，我们在此仅展示结果，并且再次证明GP方法在较低的计算时间内生成了比SAC/神经网络方法更好的控制器。下面的图表显示了未控系统的振荡、GP控制器下的振荡和SAC控制器下的振荡。

不受控制的动力，作者提供的

GP控制结果，由作者提供

作者提供的SAC控制的动力学特性

两种算法都在未受控制的动力学上有所改进。我们看到，虽然SAC控制器更快地起作用（大约在20个时间步骤时），但精度较低。然而，GP控制器需要稍长一些时间来起作用，但两个状态都表现得更加平稳。就像之前提到的那样，GP在比SAC更少的迭代中收敛。

我们已经注意到，中学可以被轻松地调整以允许在ODE系统上训练RL算法，使其适应，并简要地讨论了ODE在描述和探索RL控制下的物理动态方面的强大之处，并再次看到GP取得了更好的效果。然而，我们还没有尝试优化任一算法，只是根据对基本算法参数的猜测来进行设置。我们现在将通过扩展MGM研究来弥补这一不足。

Sagemaker使用自定义模型超参数调优

正如我们之前讨论的，GP和SAC都有定义模型的一组超参数。这些参数在训练过程中保持不变，但可以通过调整来尝试提升模型性能（比如准确率或收敛速度更快）。简单回顾一下，请参阅下表，它描述了GP算法所用的超参数。

Ni，Ne，Nn，Pr，Pm，Pc所有这些都影响探索与利用之间的平衡，即算法花费多少时间来寻找新的可能解决方案，以及精炼现有的最佳解决方案之间的平衡。N个批次通过增加计算时间来提高准确性和泛化能力。

这里实现的SAC（Soft Actor-Critic）有以下超参数：

为了简化编码和调优参数，已经设定了若干基本规则。每个隐藏层的神经元数量相同，每个神经网络（包括actor和critic这两个网络）将具有相同的维度（除了输入和输出层）以及用于更新的批处理和缓冲区。此外，所有神经网络都将使用相同的激活函数和优化器。在此为了减少代码复杂性和计算时间，我们不会调整这些参数。

调整超参数的目标是找到能够生成最准确模型同时计算成本最小的参数组合。然而，调整超参数需要为每组超参数重新训练模型。探索整个超参数空间，即使对于数量适中的超参数，如果希望对这些参数的广泛值范围进行测试，也会导致测试矩阵呈几何级数增长。这个问题变得更加复杂，因为超参数之间可能存在耦合关系（即一个参数的最佳值可能取决于另一个参数的设置）。有几种方法可以用来调整超参数。网格搜索会测试整个网格中每种可能的参数组合，需要仔细选择要测试的参数及其值。随机搜索则随机选择参数组合进行测试。最后，可以使用一些数学优化方法，例如贝叶斯优化或其他机器学习算法。无论如何，最好的方法需要仔细考虑（甚至可能涉及超超参数的优化）。

AWS Sagemaker 提供了内置的超参数优化功能，适用于 Sagemaker 自带的算法或您自定义的算法。Sagemaker 的调整选项包括随机、网格、贝叶斯或 Hyperband（Hùyínhànbān，超环带）（该方法偏向表现良好的超参数集，并且可以提前停止表现不佳的超参数集）。要使用 Sagemaker 的超参数调整功能，我们必须将算法作为 Docker 容器提供给 Sagemaker，并将这两个文件（容器镜像和训练脚本）传递给超参数调整作业。

由于既不使用GP也不使用具体的SAC实现中的现有Sagemaker算法或框架（这里使用的SAC基于Jax和Haiku，而不是tensorflow、pytorch或mxnet），我们需要创建自定义的强化学习（RL）框架。经过多次尝试和错误后，我参考了几个教程，能够成功构建用于超参数调优的工作正常的容器和训练脚本。在这一过程中遇到了几个棘手的问题；例如，我发现我需要将训练文件压缩成zip文件，上传到S3，然后将S3中zip文件的路径传递给Sagemaker的“estimator”ML对象的超参数设置，才能成功使用。Dockerfile、容器文件、训练脚本和在Sagemaker上使用的Jupyter笔记本等相关文件可在git上找到SAC和GP的链接。Git上的笔记本中提供了部分参考资料的链接。

这种方法可以进一步优化；例如，app.py 文件可能不需要打包进容器里。此外，我把自定义的 ODE 模型放在了“经典控制”环境里，并直接本地加载以减少从头构建自己环境所需的时间。

一旦容器开始运行，我参考了AWS 博客来设置超参数调整作业。为了使超参数在GP 的 app.py 和 SAC 的 sacapp.py 这两个脚本中生效，我按照Sagemaker github 示例中的说明，为参数设置了 argparse。为了减少调整作业的运行次数（并降低个人成本），我选择了有限数量的超参数来专注于该概念的探索和评估调整的效果。