PCA（主成分分析）常用于数据科学，通常用于降维（也常用于可视化），但它实际上也非常适合用于离群点检测，本文将详细介绍这一点。

这篇继续了我的离群点检测系列文章，该系列还包括关于一个Counts Outlier Detector、距离度量学习方法、共享最近邻算法以及Doping的文章。本文还包括我书《Python中的离群点检测》的一部分内容。

PCA的核心思想在于，大多数数据集在某些列上的方差远大于其他列的方差，并且特征之间也存在相关性这一点。这意味着，在表示数据时，通常不需要使用所有的特征；我们可以用较少的特征很好地近似数据——有时甚至少得多。例如，对于一个包含100个特征的数值数据表，我们可以使用可能30或40个特征来合理地表示数据，或者远少于这些。

为了做到这一点，PCA将数据转换到一个不同的坐标系统中，在这个系统中，维度被称为主成分。

由于我们经常遇到维度灾难导致的离群点检测问题，使用较少的特征可以非常有益。正如在《共享最近邻》和《用于离群点检测的距离度量学习》文章中提到的，使用大量特征会使离群点检测变得不可靠；高维数据的一个问题是，它可能导致点间距离计算不可靠（许多离群点检测器依赖于此）。PCA 可以减轻这些问题的影响。

更令人惊讶的是，使用PCA常常使得离群值更容易被发现。PCA转换通常会重组数据，使得任何异常的点更容易被发现。

这里有个例子。

    import numpy as np  
    import pandas as pd  
    from sklearn.decomposition import PCA  

    # 创建两个包含100个随机值的数组，这两个数组之间具有很强的相关性  
    x_data = np.random.random(100)   
    y_data = np.random.random(100) / 10.0  

    # 使用该数据创建一个DataFrame，并添加两个额外的数据点  
    data = pd.DataFrame({'A': x_data, 'B': x_data + y_data})   
    data = pd.concat([data,   
       pd.DataFrame([[1.8, 1.8], [0.5, 0.1]], columns=['A', 'B'])])  

    # 使用PCA将数据转换到另一个二维空间  
    pca = PCA(n_components=2)   
    pca.fit(data)  
    print(pca.explained_variance_ratio_)  

    # 创建一个新的DataFrame来存储PCA转换后的数据  
    new_data = pd.DataFrame(pca.transform(data), columns=['0', '1'])

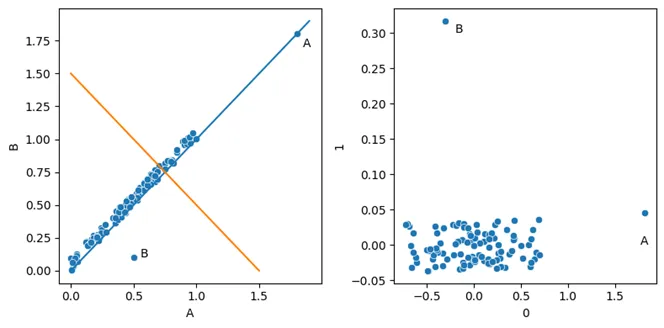
这首先创建了原始数据，如左图所示。然后使用PCA对其进行转换处理。处理完毕后，我们得到了新的空间中的数据，如右图所示。

在这里，我创建了一个简单的合成数据集，数据间高度相关。这里有两个异常值，其中一个非常极端但符合总体趋势（点A），另一个虽然各维度值均为正常范围，但并不符合总体趋势（点B）。

我们然后使用 scikit-learn 的 PCA 类来转换数据集。转换后的数据会被放入另一个 pandas 数据框中，然后可以像下图那样绘制出来，或者检查异常值或进行分析。

查看原始数据，数据呈现出沿对角线分布的趋势。从左下角到右上角画一条线（图中蓝色的线，如左图所示），我们可以用它来定义一个新的维度，该维度很好地代表了数据。事实上，当我们进行PCA时，这将是第一个主成分，而垂直这条线（图中橙色的线）将是第二个主成分，用于表示剩余的方差。

有了更加真实的数据，我们不会拥有如此强烈的线性关系，但特征之间通常存在一些关联性——特征完全独立的情况很少见。基于这一点，PCA通常可以有效地降低数据集的维度。也就是说，虽然通常需要所有成分来完全描述每个项目，使用部分成分通常足以描述几乎所有的记录。

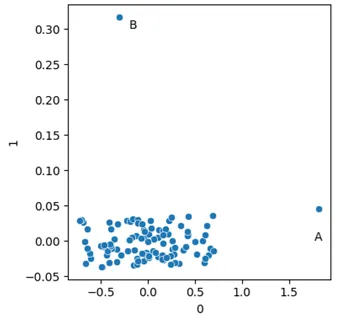
右侧的面板显示了由PCA变换创建的新空间中的数据，其中第一个分量（捕捉到大部分方差）位于x轴上，第二个分量（捕捉到剩余的方差）位于y轴上。对于二维数据而言，PCA变换会简单地旋转并拉伸数据。在更高维度上，变换更难可视化，但其工作原理大致相同。

打印解释的方差（上面的代码包含了一个打印语句来显示这一点）表明，第 0 个分量包含了 0.99 的方差，正如第 1 个分量则包含了 0.01 的方差，这与图表非常吻合。

通常会逐个检查组件（如直方图），但在本例中，我们采用散点图，这样可以节省空间，因为我们可以通过一张图查看两个组件。异常值会在两个组件中很明显。

仔细看看PCA的工作原理，它首先找到一条能最好地描述数据的直线，使得所有点到该直线的平方距离之和最小。这就得到了第一主成分。接着，找到一条与之正交的直线，这条直线最好地捕获剩余的方差。由于这个数据集只有两个维度，因此第二个主成分的方向自然就是与第一个主成分垂直。

当原始数据的维度更多时，此过程将进行一些额外的步骤：该过程会一直持续到捕获数据中的所有方差为止，这将创建与原始数据维度数量相同的成分。基于此，PCA具有三个特点。

• 所有组件之间都不相关。
• 第一个组件的变异程度最大，然后是第二个，以此类推。
• 所有组件的总变异程度等于原始特征的总方差。

PCA还有一些很好的特性，非常适合检测异常值。如图所示，异常值在各个成分中得到了很好的隔离，这样我们就可以用简单的测试来识别它们。

我们还可以看到PCA转换的另一个有趣结果：符合总体模式的点往往会落在早期的主成分上，但可能会在这些主成分上达到极端值（如点A），而不符合数据总体模式的点则往往不会落在主成分上，而是在后面的主成分上成为极端值（如点B）。

用PCA来识别异常值，通常有以下两种常见方法：

• 我们可以使用PCA转换数据，然后对每个分量进行一系列测试，为每一行打分。这很容易实现，代码也很简洁。
• 从图中可以看出，仅用第一个分量就能很好地描述大部分数据。要完全描述所有数据，则需要第二个分量。但是，我们就能大致描述大部分数据的位置。例外是点B；它在第一个分量上的位置并不能很好地描述其全部位置，如果仅使用一个分量来重建该点的位置，误差会很大，而对于其他点则不是这样。一般来说，描述一个点的位置所需分量越多（或者给定分量数量下的误差越大），该点就越像是一个异常值。

另一种方法是一次移除一行，并找出哪些行对最终的PCA计算影响最大。虽然这种方法可以有效，但是通常速度较慢，不常被使用。我可能在以后的文章中介绍这种方法，但本文将讨论重建误差，下一篇文章将对PCA组件进行简单的测试。

重构误差是在离群点检测中常用的一种通用方法的例子。我们通过各种方式建模数据，以捕捉数据中的主要特征（例如，使用常见的项目集合、聚类、建立预测模型来从其他列预测每一列等）。这些模型将倾向于很好地拟合大部分数据，但通常对离群点的覆盖不够好。这些记录将无法很好地融入模型。这样的记录可能无法很好地由常见的项目集合表示，无法放入任何聚类中，或者该记录中的值无法很好地从其他值中预测出来。在这种情况下，离群点就是那些难以用第一个主成分分析的结果表示的数据点。

PCA 假设特征之间存在关联性。上述数据可以通过转换使得第一个主成分捕捉到比第二个主成分更多的方差，因为这些数据之间存在相关性。当特征之间没有关联时，PCA 对离群值检测的帮助很小，但是由于大多数数据集都具有显著的相关性，因此 PCA 非常实用。鉴于此，我们通常可以找到一个相对较少的主成分数量来捕捉数据集中的大部分方差。

与用于离群点检测的其他一些常见技术（包括椭圆包络方法、高斯混合模型（GMM）和马氏距离（Mahalanobis距离）计算）类似，PCA通过创建表示数据整体形状的协方差矩阵来实现，然后用该矩阵进行空间转换。事实上，椭圆包络方法、马氏距离和PCA之间有很强的关联性。

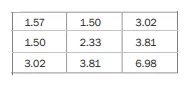
协方差矩阵是一个 d x d 的矩阵（其中 d 代表数据中的特征或维度的数量），它存储每对特征之间的协方差，每个特征的方差位于主对角线上（也就是说，每个特征与自身的协方差）。协方差矩阵和数据中心一起可以简洁地描述数据——即，通常可以很好地描述数据，每个特征的方差和特征之间的协方差。

一个具有三个特征的数据集的协方差矩阵可能看起来像这样：

这里有一个数据集的示例协方差矩阵，这个数据集有三个特征。

在这里显示了三个特征的方差值，位于主对角线上：1.57、2.33、和6.98。我们还有每个特征之间的协方差值。例如，第一个和第二个特征之间的协方差值为1.50。矩阵关于主对角线对称，因为协方差值是对称的，以此类推。

Scikit-learn（以及其他包）提供了计算任意给定数值数据集协方差矩阵的工具，但使用本文和下一篇文章中描述的技术直接计算这些是没有必要的。本文探讨了一个名为PyOD的流行包所提供的工具，该包（可能是目前在Python中用于表格数据异常值检测最完整和最常用工具之一）。这些工具为我们自动处理PCA变换并进行异常值检测。

PCA的一个限制是，它对离群点非常敏感。它是通过最小化点到各分量的平方距离实现的，因此这种方法很容易受到离群点的影响（离群点可能会产生非常大的平方距离）。为了解决这个问题，通常会采用鲁棒PCA，在这种方法中，会在进行变换之前移除每个维度上的极端值。下面的例子中包含了这种方法，这展示了如何处理离群点。

PCA（以及 Mahalanobis 距离和类似方法）的另一个局限是，当相关性仅存在于数据的某些区域时，PCA 可能会失效，这种情况在数据聚类时非常普遍。当数据聚类良好时，可能首先需要对数据进行聚类，或者说是分割，然后再对每个子集分别进行 PCA 分析。

现在我们已经了解了PCA的工作原理，以及它在高层次上如何用于异常检测，我们现在来看看PyOD提供的那些检测器。

PyOD实际上提供了三种基于PCA的类：PyODKernelPCA、PCA 和 KPCA。我们将逐一探讨这些类。

PyOD 提供了一个名为 PyODKernelPCA 的类，它只是 scikit-learn 的 KernelPCA 类的一个包装器。在不同情况下使用更方便。本身它并不作为一个异常检测器，而是提供了与 scikit-learn 的 PCA 类类似的主成分分析变换及其逆变换，在之前的例子中已经使用过的那种。

KernelPCA类与PCA类不同，KernelPCA类允许对数据进行非线性变换，能够更好地捕捉某些更复杂的关系。在这个上下文中，核函数与支持向量机（SVM）模型中的表现类似：它们高效地变换空间，从而让异常值更容易被区分出来。

Scikit-learn 提供了几种内核。这些内容超出了本文的范围，但在特征之间存在复杂非线性关系时，可以改进 PCA 过程。如果使用了这些内核，离群点检测也能正常工作，否则与使用 PCA 类时一样。也就是说，我们可以在转换后的空间中直接进行离群点检测，或者测量重构误差。

先前的方法，即在变换后的空间上进行测试，既直接又有效。我们将在下一篇文章中进一步讨论。后一种方法，检查重构误差，则稍微难一些。但这并不难处理，接下来我们要探讨的由PyOD提供的两个检测器替我们做了大部分工作。

PyOD提供了两种基于PCA的离群点检测器：PCA类和KPCA。后者，类似于PyOD中的PyODKernelPCA，能够处理更复杂数据的核方法。PyOD建议在数据具有线性关系时使用PCA类，否则使用KPCA。

两个类都使用数据的重建误差，通过计算点到由前k个主成分构建的超平面的欧氏距离来衡量。想法在于，前k个成分很好地捕捉了数据的主要模式，而不能由这些成分很好地建模的点则被视为离群点。

在上面的图中，这不会捕捉到点A，但会捕捉到点B。如果我们把k设为1，那么我们只会使用第一个成分，并测量每个点从其实际位置到这个成分上位置的距离。点B的距离会比较大，因此可以被标记为离群点。

在处理PCA数据时，通常也是这样，最好在拟合数据之前移除任何明显的离群点。在下面的例子中，我们使用PyOD提供的另一个检测器ECOD（经验累积分布函数）来达到这个目的。ECOD可能你不太熟悉，但它真的很厉害。事实上，PyOD建议，在为项目选择检测器时，最好从孤立森林和ECOD开始。

ECOD 本文不讨论。它在《Python中的离群点检测》这本书中有详细讲解，PyOD 也提供了原始期刊论文的链接。但作为简要概述：ECOD 旨在识别数值列中的极端（非常小和非常大）值，并设计用于找出这些极端值。它不检查值的稀有组合，仅关注极端值。因此，它不能找到所有离群点，但它速度非常快，且能很好地发现这种类型的离群点。在这种情况下，我们在使用 PCA 检测器之前，移除了 ECOD 标记的顶部 1% 的行。

通常在进行离群点检测（而不仅是在使用主成分分析PCA时），首先清理数据是有用的，这在离群点检测的背景下通常指移除明显的异常值。这使离群点检测算法能更好地适应典型数据，从而更好地捕捉数据中的主要模式（从而使它能够更好地识别这些主要模式的例外情况）。在这种情况下，清理数据使得主成分分析计算可以在更典型的数据上进行，以便更好地反映数据的主要分布。

在执行之前，需要安装PyOD，可以通过以下方法安装。

    pip install pyod

此处使用的代码使用了OpenML上的speech数据集（公共许可证），该数据集包含400个数值特征。也可以使用任何数值数据集（任何分类列都需要进行编码处理）。同样，数值特征通常需要进行缩放，以使其与其他特征具有相同的尺度（此处省略不谈，因为这里所有特征使用相同的编码）。

    import pandas as pd  
    from pyod.models.pca import PCA  
    from pyod.models.ecod import ECOD  
    from sklearn.datasets import fetch_openml  

    # A. 收集数据， 
    data = fetch_openml("speech", version=1, parser='auto')   
    df = pd.DataFrame(data.data, columns=data.feature_names)  
    scores_df = df.copy()  

    # 创建一个ECOD检测器来清理数据  
    clf = ECOD(contamination=0.01)   
    clf.fit(df)  
    scores_df['ECOD Scores'] = clf.predict(df)  

    # 创建一个经过清理的数据版本，移除ECOD检测到的异常值  
    clean_df = df[scores_df['ECOD Scores'] == 0]   

    # 对清理后的数据训练一个PCA检测器  
    clf = PCA(contamination=0.02)   
    clf.fit(clean_df)  

    # 对全部数据进行预测  
    pred = clf.predict(df) 

运行这段代码之后，pred变量将包含数据中每个记录的异常值得分，例如。

KPCA检测器的工作方式与PCA检测器非常类似，唯一的不同在于它会在数据上应用一个指定的核函数。这可以显著改变数据。这两种检测器可能会标记出完全不同的记录，由于两者都难以解释，所以很难找出原因。就像在异常值检测中一样，可能需要一些试验来找到最适合您的数据的检测器和参数。由于两者都相当强大，同时使用它们可能效果更佳。最好通过掺杂技术（如同Doping：一种测试异常值检测器的技术一文所述）来确定这一点（以及要使用的最佳参数）。

使用线性核的KPCA检测器的创建代码如下所示的代码：

# 实际代码应与上下文相关

    det = KPCA(kernel='linear')

KPCA也支持多项式，还包括径向基函数（RBF）、Sigmoid函数和余弦核函数等等。

在这篇文章中，我们探讨了主成分分析（PCA）的概念及其在异常值检测中的作用，特别是关注了PCA转换后的数据的标准异常值检测和重建误差。我们还介绍了PyOD提供的两个异常值检测器，一个是基于PCA（均使用重建误差），另一个基于核PCA（KPCA），并提供了一个基于PCA的示例。

基于PCA的异常检测方法可以非常有效，但解释性较差。PCA及其核版本KPCA检测器识别出的异常数据点非常难以理解。

事实上，即使使用可解释的离群点检测器（如计数异常值检测器，或基于z-score或四分位范围的测试），在对经过PCA转换后的数据进行检测（我们将在下一篇中讨论）时，离群点也可能是难以理解的，因为PCA转换本身（及其生成的成分）几乎是无法理解的。不幸的是，这种情况在离群点检测中很常见。离群点检测中使用的其他主要工具，包括孤立森林（Isolation Forest）、局部离群点因子（LOF）、K近邻（KNN）等大多数工具，本质上也是黑箱模型（虽然它们的算法很容易理解——但给个别记录分配的具体分数可能难以理解）。

在上面的二维示例中，查看经过PCA变换后的空间时，我们可以很容易地识别出点A和点B是离群点，但很难理解这两个轴所代表的两个成分。

在需要可解释性的情况下，可能无法使用基于PCA的方法进行解释。而在解释性不是必需的地方，基于PCA的方法在这种情况下可以非常有效。另外，PCA的可解释性并不比大多数异常检测器低；不幸的是，只有少数异常检测器能够提供较高的可解释性。

在接下来的文章中，我们将进一步看看在PCA变换后的空间中执行测试的情况。这包括简单的单变量检验，以及其他标准的异常值检测方法，同时考虑所需的时间（包括PCA变换、模型拟合和预测的时间），以及准确性。使用PCA通常可以加快异常值检测的速度，减少内存使用，并提高准确性。

这些图片都是作者拍的