人工智能学习
【综合评价方法】常见综合评价方法及其实现
@TOC
1.数据预处理
1.1 区分指标的属性
- 正向指标
- 负向指标
- 中间型指标
- 区间型指标
1.2 指标正向化
1.2.1 负向指标
负向指标的正向化方法,又称为指标反转方法,是指将原本反映负面情况的指标转换为反映正面情况的指标,以便于比较及分析。该方法广泛应用于评估指标、市场研究、数据分析等领域。
具体来说,负向指标的正向化方法可以分为以下几个步骤:
- 确定要进行正向化的指标
- 确定负向指标需要进行什么样的正向化,常见的方法包括倒数、对数、绝对值等
- 进行指标正向化的计算公式,根据不同的正向化方法而定
- 对正向化后的指标进行归一化处理,使其可比较性更强
下面介绍一种负向指标的正向化方法。
对于一组负向指标数据:
y1,y2,...,yn y_{1},y_{2},...,y_{n} y1,y2,...,yn
取出最大值:
ymax=max{y1,y2,...,yn} y_{max}=\max\left \{ y_{1},y_{2},...,y_{n} \right \} ymax=max{y1,y2,...,yn}
然后利用这个值逐个更新yiy_{i}yi :
yi:=ymax−yi y_{i}:=y_{max}-y_{i} yi:=ymax−yi
1.2.2 中间指标
中间型指标是指指标的值不要太小也不要太大,取某个特定值最好,如水体的ph值最好为7。下面介绍一种中间型指标的正向化方法:
对于一组中间型指标数据:
y1,y2,...,yn y_{1},y_{2},...,y_{n} y1,y2,...,yn
先拟定一个最优值:
ybest y_{best} ybest
然后计算这组数据中每个数据到这个最优值的距离,取出最大的那个:
M=max{∣y1−ybest∣,∣y2−ybest∣,...,∣yn−ybest∣} M=\max\left \{ \left | y_{1} -y_{best}\right |, \left | y_{2} -y_{best}\right | , ... , \left | y_{n} -y_{best}\right | \right \} M=max{∣y1−ybest∣,∣y2−ybest∣,...,∣yn−ybest∣}
然后利用这个值逐个更新yiy_{i}yi:
yi:=1−∣yi−ybest∣M y_{i}:=1-\frac{ \left | y_{i} -y_{best}\right | }{ M } yi:=1−M∣yi−ybest∣
1.2.3 区间指标
区间型指标是指,指标值落在某个区间最好,例如,人的体温在36∘C36^{\circ}C36∘C到37∘C37^{\circ}C37∘C最好。下面介绍一种区间型指标的正向化方法:
对于一组区间型指标数据:
y1,y2,...,yn y_{1},y_{2},...,y_{n} y1,y2,...,yn
先拟定一个最优区间:
(a,b) \left( a,b \right) (a,b)
取出这组数据的最大值和最小值:
ymax=max{y1,y2,...,yn},ymin=min{y1,y2,...,yn} y_{max}=\max\left \{ y_{1},y_{2},...,y_{n} \right \} , y_{min}=\min\left \{ y_{1},y_{2},...,y_{n} \right \} ymax=max{y1,y2,...,yn},ymin=min{y1,y2,...,yn}
然后计算一个值MMM:
M=max{a−ymin,ymax−b} M=\max\left \{ a-y_{min},y_{max}-b \right \} M=max{a−ymin,ymax−b}
然后用如下公式逐个更新yiy_{i}yi:
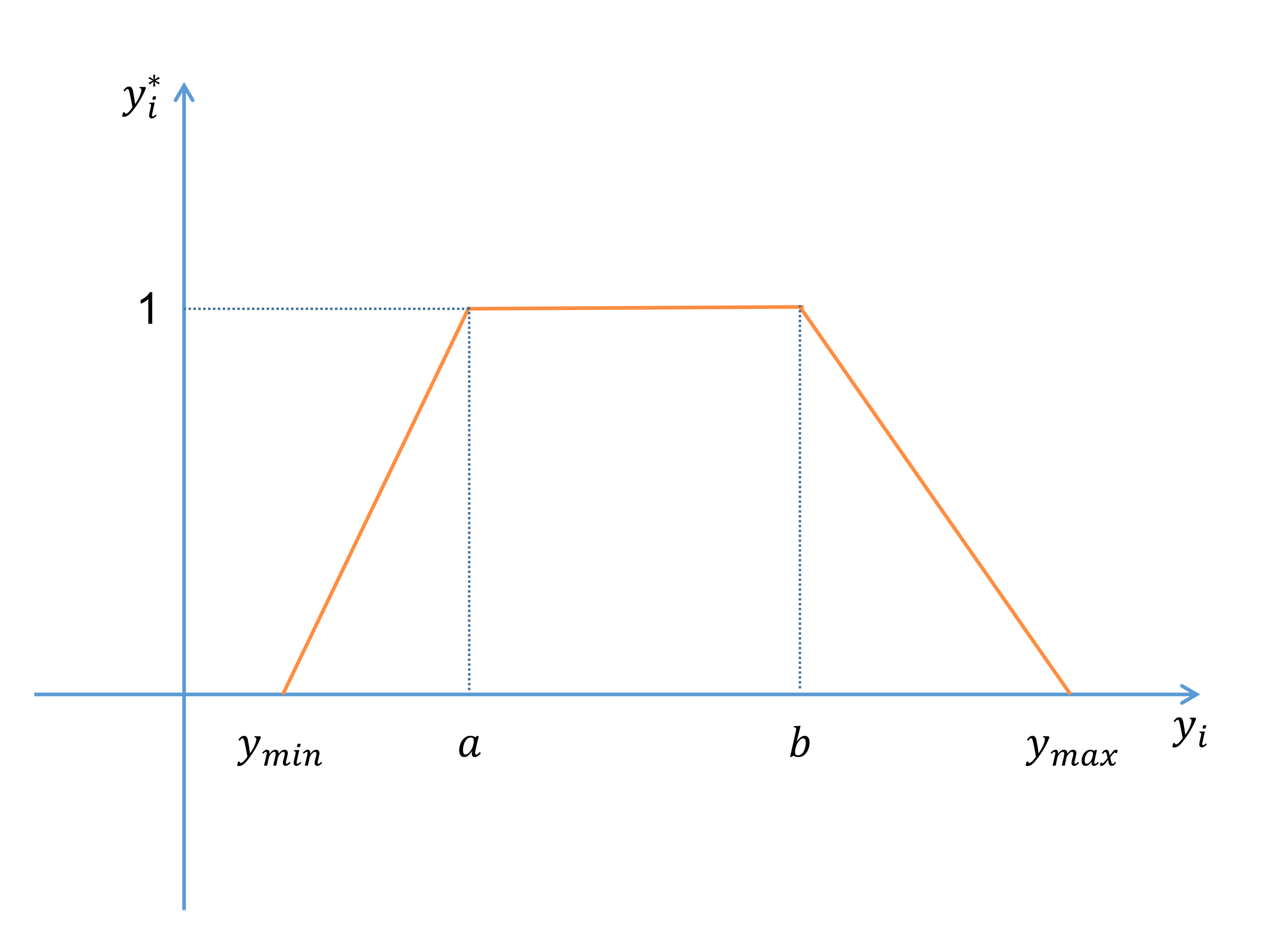
yi:={1−a−yia−ymin,ymin≤yi<a1,a≤yi≤b1−yi−bymax−b,b<yi≤ymax y_{i}:= \left\{\begin{matrix} 1-\frac{a-y_{i}}{a-y_{min}},y_{min} \le y_{i} < a \\ 1,a \le y_{i} \le b \\ 1-\frac{y_{i}-b}{y_{max}-b},b < y_{i} \le y_{max} \end{matrix}\right. yi:=⎩⎨⎧1−a−ymina−yi,ymin≤yi<a1,a≤yi≤b1−ymax−byi−b,b<yi≤ymax
用如下这个梯形图表示更为直观:
1.3 标准化
1.3.1 Z-score 标准化
对于样本 XXX 中的每个特征:
Xnormalized=(X−μ)σ X_{normalized} = \frac{(X - \mu)}{\sigma} Xnormalized=σ(X−μ)
其中,μ\muμ 是该特征的平均值,σ\sigmaσ 是该特征的标准差。
1.3.2 Min-max 标准化
对于样本 XXX 中的每个特征:
Xnormalized=(X−Xmin)(Xmax−Xmin) X_{normalized} = \frac{(X - X_{min})}{(X_{max} - X_{min})} Xnormalized=(Xmax−Xmin)(X−Xmin)
其中,XminX_{min}Xmin 是该特征的最小值,XmaxX_{max}Xmax 是该特征的最大值。
1.3.3 Robust 标准化
对于样本 XXX 中的每个特征:
Xnormalized=(X−median)IQR/2 X_{normalized} = \frac{(X - median)}{IQR/2} Xnormalized=IQR/2(X−median)
其中,median 是该特征的中位数,IQR 是四分位数范围(即上四分位数和下四分位数之差)。
1.3.4 归一化
对于样本 XXX 中的每个特征:
Xnormalized=X∑i=1nxi2 X_{normalized} = \frac{X}{\sqrt{\sum_{i=1}^{n}x_i^2}} Xnormalized=∑i=1nxi2X
其中,nnn 是该样本的特征数量。
2.模糊评价法(主观)(not recommended)
- 适用于未给出指标的评价问题
3.层次分析法(主观)(not recommended)
- 适用于未给出指标的评价问题
4.PCA主成分分析法(客观)
主成分分析法是一种常用的无监督降维技术,它将原始数据投影到一个新的低维度空间中,以便保留数据的最大方差。通过选择适当数量的主成分,我们可以捕捉到数据中最重要的信息,并且减少原始数据的维度。
4.1 步骤
- 数据正向化、标准化:假设我们有ppp维度的样本数据KaTeX parse error: Expected 'EOF', got '\boldsymbol' at position 1: \̲b̲o̲l̲d̲s̲y̲m̲b̲o̲l̲{X}=(\boldsymbo…,每一维度的数据均值为0,标准差为1。这一步的目的是为了除去维度间的量纲影响。
KaTeX parse error: Expected 'EOF', got '\boldsymbol' at position 2: \̲b̲o̲l̲d̲s̲y̲m̲b̲o̲l̲{x}_j' = \frac{…
其中,KaTeX parse error: Expected '}', got '\boldsymbol' at position 6: \bar{\̲b̲o̲l̲d̲s̲y̲m̲b̲o̲l̲{x}}是所有样本数据的均值,σj\sigma_jσj是第jjj维度的标准差。
-
计算协方差矩阵:计算标准化后数据的协方差矩阵。协方差矩阵描述了不同特征之间的相关性。
公式:
Σ=1n−1(X−X¯)T(X−X¯) \Sigma = \frac{1}{n-1}(X-\bar{X})^T(X-\bar{X}) Σ=n−11(X−X¯)T(X−X¯)
其中,Σ\SigmaΣ 是协方差矩阵,XXX 是标准化后的数据矩阵,X¯\bar{X}X¯ 是每个特征的均值,nnn 是样本数量。
-
计算特征值和特征向量:对协方差矩阵进行特征值分解,得到特征值和对应的特征向量。特征向量表示了数据在新的特征空间中的方向。
-
选择主成分:按照特征值的大小对特征向量进行排序,选择前k个特征向量作为主成分。这些主成分对应的特征值较大,包含了较多的原始数据信息。
-
计算投影:将原始数据投影到选定的主成分上,得到降维后的数据。
公式:
Y=XstdW Y = X_{\text{std}}W Y=XstdW
其中,YYY 是降维后的数据矩阵,XstdX_{\text{std}}Xstd 是标准化后的数据矩阵,WWW 是前k个特征向量组成的投影矩阵。
-
可选:重构数据:根据降维后的数据和投影矩阵,可以通过逆变换将数据重新映射到原始空间中。
公式:
Xreconstructed=YWT X_{\text{reconstructed}} = YW^T Xreconstructed=YWT
其中,XreconstructedX_{\text{reconstructed}}Xreconstructed 是重构后的数据矩阵。
4.2 实现
>>> import numpy as np
>>> from sklearn.decomposition import PCA
# 输入待降维数据 (5 * 6) 矩阵,6个维度,5个样本值
>>> A = np.array([[84,65,61,72,79,81],[64,77,77,76,55,70],[65,67,63,49,57,67],[74,80,69,75,63,74],[84,74,70,80,74,82]])
>>> print(A)
[[84 65 61 72 79 81]
[64 77 77 76 55 70]
[65 67 63 49 57 67]
[74 80 69 75 63 74]
[84 74 70 80 74 82]]
# 直接使用PCA进行降维
>>> pca = PCA(n_components=2) #降到 2 维
>>> pca.fit(A)
PCA(n_components=2)
>>> pca.transform(A) # 降维后的结果
array([[-16.14860528, -12.48396235],
[ 10.61676743, 15.67317428],
[ 23.40212697, -13.607117 ],
[ -0.43966353, 7.77054621],
[-17.43062559, 2.64735885]])
>>> pca.explained_variance_ratio_ # 降维后的各主成分的方差值占总方差值的比例,即方差贡献率
array([0.63506778, 0.339022 ])
>>> pca.explained_variance_ # 降维后的各主成分的方差值
array([306.29319053, 163.51030959])
5.Topsis方法(客观)
Topsis综合评价方法是一种多维决策分析方法,适用于多种复杂的评估和决策场景中。为了更清楚地解释,我将对每个步骤进行更详细的说明。
首先,评估方案需要同时考虑多个评价指标,这些指标可能相互矛盾或者有不同的权重,需要通过一定的数学模型将其标准化处理,并根据相对重要性进行加权计算。Topsis方法正是基于这个框架,采用了以下的计算方法来求出每个方案在各个指标上的综合得分。
5.1 正向化
详见1.2
5.2 标准化
一般使用1.3.4的归一方法。
假设有n个方案(或实体),每个方案有m个不同的评价指标,在不同的评价指标间进行综合评估。对于每一个方案i的j指标可以通过以下的计算得到其标准化后的数值v(i,j):
vij=xij∑i=1nxij2 v_{ij} = \frac{x_{ij}}{\sqrt{\sum_{i=1}^n{x^2_{ij}}}} vij=∑i=1nxij2xij
其中 xijx_{ij}xij 表示第i个方案的第j项指标原始数据。标准化处理将不同维度的数据范围统一到0-1之间,并且会消除数据量级之间的影响。
5.3 计算正负理想解
- 如果没有进行正向化:
对于利益类指标,如价格、收益等,需要最大化;而对于成本类指标,如成本、负债等,需要最小化。可以分别计算出每一个指标在给定n个方案中的最大值和最小值。设 第j项指标的正理想解为vj+v^{+}_{j}vj+, 负理想解为vj−v^{-}_{j}vj−。具体的计算方式如下所示:
对于利益类指标:
vj+=max{vij∣i=1,2,⋯,n} v^{+}_{j} = \max{\{v_{ij}| i = 1, 2, \cdots, n\}} vj+=max{vij∣i=1,2,⋯,n}
vj−=min{vij∣i=1,2,⋯,n} v^{-}_{j} = \min{\{v_{ij}| i = 1, 2, \cdots, n\}} vj−=min{vij∣i=1,2,⋯,n}
对于成本类指标:
vj+=min{vij∣i=1,2,⋯,n} v^{+}_{j} = \min{\{v_{ij}| i = 1, 2, \cdots, n\}} vj+=min{vij∣i=1,2,⋯,n}
vj−=max{vij∣i=1,2,⋯,n} v^{-}_{j} = \max{\{v_{ij}| i = 1, 2, \cdots, n\}} vj−=max{vij∣i=1,2,⋯,n}
- 如果进行了正向化:
取每个列向量的最大值即可。
5.4 计算每个方案与正负理想解的距离
在标准化之后,可以对每一个方案与正负理想解之间的距离进行计算。设第i个方案到正理想解的距离为Si+S_{i}^{+}Si+, 到负理想解的距离为Si−S_{i}^{-}Si−。
Si+=∑j=1m(vij−vj+)2 S^{+}_{i} = \sqrt{\sum_{j=1}^m{(v_{ij}-v^{+}_{j})}^{2}} Si+=j=1∑m(vij−vj+)2
Si−=∑j=1m(vij−vj−)2 S^{-}_{i} = \sqrt{\sum_{j=1}^m{(v_{ij}-v^{-}_{j})}^{2}} Si−=j=1∑m(vij−vj−)2
其中,mmm为指标维度的数量。 Si+S^{+}_{i}Si+表示方案iii与正理想解之间的距离,Si−S^{-}_{i}Si−表示方案iii与负理想解之间的距离,值越小越接近理想解,因此可以把正负理想解的范围展开到[0,1][0, 1][0,1]之间作为检验指标的依据.
5.5 计算综合得分
最终的综合得分sis_isi可以通过权衡每个指标从而得到,如下所示:
si=Si−Si++Si− s_{i} = \frac{S^{-}_{i}}{S_{i}^{+}+S_{i}^{-}} si=Si++Si−Si−
其中,Si+S_{i}^{+}Si+表示第iii个方案与正理想解的距离,Si−S_{i}^{-}Si−表示第iii个方案与负理想解的距离。综合得分sis_isi可以看作是评价指标的加权平均值。当综合得分越高时,则表示第iii个方案越更优。
下面举一个例子来说明如何使用这种方法进行决策。例如,一家公司想在考虑多个指标情况下选择最适合的机器学习平台。他们的评价指标包括特性得分(例如各种模型类型的大小、精度等),服务质量得分(包括易用性、响应时间、数据隐私度,等等),价格得分等。我们假设有三个候选机器学习平台,评价指标如下表所示:
| 候选平台 | 特性得分(0 - 1) | 服务质量得分(0 - 1) | 价格得分(0 - 1) |
|---|---|---|---|
| 平台 A | 0.8 | 0.6 | 0.7 |
| 平台 B | 0.6 | 0.8 | 0.6 |
| 平台 C | 0.7 | 0.5 | 0.8 |
使用 Topsis 方法来计算得到每个平台的得分:
对每个评价指标进行标准化,计算符合每个标准化指标的正负理想解,计算每个平台到理想解的距离:
| 候选平台 | 特性得分 | 服务质量得分 | 价格得分 | 正理想解 | 负理想解 | 到正理想解的距离 | 到负理想解的距离 | 综合得分 |
|---|---|---|---|---|---|---|---|---|
| 平台 A | 0.8 | 0.6 | 0.7 | 0.8 | 0.5 | 0.2236 | 0.3606 | 0.3825 |
| 平台 B | 0.6 | 0.8 | 0.6 | 0.8 | 0.5 | 0.2828 | 0.2828 | 0.5000 |
| 平台 C | 0.7 | 0.5 | 0.8 | 0.8 | 0.5 | 0.2449 | 0.3317 | 0.4255 |
通过计算得出, 平台 B 的综合得分最高,因此可以推荐该平台作为其机器学习的首选选项。
6.灰色关联分析法(客观)
灰色关联度分析是一种比较常用的多因素综合评价方法,它可以用于确定不同的对象与某一参考对象之间关联度。如果我们把这个参考对象设置为理想中的完美对象,那么灰色关联分析法就可以分析出不同的对象的优劣。
具体实施步骤如下:
6.1 收集数据
建立评价指标矩阵,其中每行对应一个因素(评价对象),每列对应一个评价指标。评价指标可以是数量指标,也可以是质量(定性)指标,但是指标之间的具体意义必须相同。设评价指标矩阵为 XXX,其中 xijx_{ij}xij 表示第 iii 个因素对第 jjj 个指标的值。
我们先给出一个例子,某核心企业待选供应商的指标评价有关数据:
| 评价指标 | 对象1 | 对象2 | 对象3 | 对象4 | 对象5 | 对象6 |
|---|---|---|---|---|---|---|
| 产品质量 | 0.83 | 0.90 | 0.99 | 0.92 | 0.87 | 0.95 |
| 产品价格(元) | 326 | 295 | 340 | 287 | 310 | 303 |
| 地理位置(千米) | 21 | 38 | 25 | 19 | 27 | 10 |
| 售后服务(小时) | 3.2 | 2.4 | 2.2 | 2.0 | 0.9 | 1.7 |
| 技术水平 | 0.20 | 0.25 | 0.12 | 0.33 | 0.20 | 0.09 |
| 经济效益 | 0.15 | 0.20 | 0.14 | 0.09 | 0.15 | 0.17 |
| 供应能力(件) | 250 | 180 | 300 | 200 | 150 | 175 |
| 市场影响度 | 0.23 | 0.15 | 0.27 | 0.30 | 0.18 | 0.26 |
| 交货情况 | 0.87 | 0.95 | 0.99 | 0.89 | 0.82 | 0.95 |
6.2 正向化和标准化并建立参考对象
对评价指标矩阵进行正向化和标准化,将各项指标转化为同一量纲下的评价指标值。其中标准化方法一般采用Min-max标准化。详见1.2与1.3。
在上面这个例子中,产品价格、地理位置、售后服务是负向指标,其他都是正向指标。预处理后的数据如下:
| 评价指标 | 对象1 | 对象2 | 对象3 | 对象4 | 对象5 | 对象6 |
|---|---|---|---|---|---|---|
| 指标1 | 0 | 0.4375 | 1 | 0.5625 | 0.25 | 0.75 |
| 指标2 | 0.2642 | 0.8491 | 0 | 1 | 0.566 | 0.6981 |
| 指标3 | 0.6071 | 0 | 0.4643 | 0.6786 | 0.3929 | 1 |
| 指标4 | 0 | 0.3478 | 0.4348 | 0.5217 | 1 | 0.6522 |
| 指标5 | 0.4583 | 0.6667 | 0.125 | 1 | 0.4583 | 0 |
| 指标6 | 0.5455 | 1 | 0.4545 | 0 | 0.5455 | 0.7273 |
| 指标7 | 0.6667 | 0.2 | 1 | 0.3333 | 0 | 0.1667 |
| 指标8 | 0.5333 | 0 | 0.8 | 1 | 0.2 | 0.7333 |
| 指标9 | 0.2941 | 0.7647 | 1 | 0.4118 | 0 | 0.7059 |
建立参考对象,如下:
| 评价指标 | 对象1 | 对象2 | 对象3 | 对象4 | 对象5 | 对象6 | 参考对象 |
|---|---|---|---|---|---|---|---|
| 指标1 | 0 | 0.4375 | 1 | 0.5625 | 0.25 | 0.75 | 1 |
| 指标2 | 0.2642 | 0.8491 | 0 | 1 | 0.566 | 0.6981 | 1 |
| 指标3 | 0.6071 | 0 | 0.4643 | 0.6786 | 0.3929 | 1 | 1 |
| 指标4 | 0 | 0.3478 | 0.4348 | 0.5217 | 1 | 0.6522 | 1 |
| 指标5 | 0.4583 | 0.6667 | 0.125 | 1 | 0.4583 | 0 | 1 |
| 指标6 | 0.5455 | 1 | 0.4545 | 0 | 0.5455 | 0.7273 | 1 |
| 指标7 | 0.6667 | 0.2 | 1 | 0.3333 | 0 | 0.1667 | 1 |
| 指标8 | 0.5333 | 0 | 0.8 | 1 | 0.2 | 0.7333 | 1 |
| 指标9 | 0.2941 | 0.7647 | 1 | 0.4118 | 0 | 0.7059 | 1 |
由于此处进行了正向化处理和Min-max标准化,因此,此处的参考对象的各项指标只要对每一行都取最大值即可。
6.3 确定权重
确定各个指标对应的权重。但暂时不对指标矩阵的每一行进行加权处理。可用层次分析法确定这些权值。
ω=[ω1,ω2,...,ωn],∑i=1nωi=1 \omega =\left [ \omega _{1} ,\omega _{2} ,...,\omega _{n}\right ] ,\sum_{i=1}^{n} \omega _{i}=1 ω=[ω1,ω2,...,ωn],i=1∑nωi=1
这些权值将在计算灰色关联度的时候用到。
6.4 计算灰色关联系数
我们记xix_{i}xi为对象iii,参考对象为x0x_{0}x0。xix_{i}xi与x0x_{0}x0都有m个指标,我们需要求出它们在第k个指标上的关联系数。关联系数越大,代表这个实际对象越贴近于参考对象。对于n个实际对象,m个指标,xi(j)x_{i}(j)xi(j)表示实际对象i的第j个指标的值,那么,xix_{i}xi与x0x_{0}x0在第k个指标上的关联系数的计算公式如下:
KaTeX parse error: Expected '}', got '\\' at position 118: …}(t) \right | \̲\̲ …
其中,min1≤s≤nmin1≤t≤m∣x0(t)−xs(t)∣\min_{1\le s \le n} \min_{1\le t \le m} \left | x_{0}(t)-x_{s}(t) \right |min1≤s≤nmin1≤t≤m∣x0(t)−xs(t)∣称为两极最小差,max1≤s≤nmax1≤t≤m∣x0(t)−xs(t)∣\max_{1\le s \le n} \max_{1\le t \le m} \left | x_{0}(t)-x_{s}(t) \right |max1≤s≤nmax1≤t≤m∣x0(t)−xs(t)∣称为两级最大差,ρ\rhoρ称为分辨系数。
两级最小差和两级最大差的计算过程,就是把指标矩阵的各个值与参考对象进行比较的过程。分辨系数ρ\rhoρ越大,分辨率就越大;ρ\rhoρ越小,分辨率就越小
在上面的例子中,我们可以算出两级最小差为0,两级最大差为1。这是由于使用了Min-max标准化方法而导致的。
6.5 计算灰色加权关联度并排序
灰色加权关联度就是每个对象的最终得分,它采用如下公式计算:
ri=∑k=1nwiξi(k) r_{i}=\sum_{k=1}^{n}w_{i}\xi _{i}(k) ri=k=1∑nwiξi(k)
其中,rir_{i}ri 表示待评价对象的得分,wiw_{i}wi是6.3中确定的权值。
最终按照各个评价对象的得分进行排序,得分高表示与各项指标的关系越密切,也就越好。
本文由博客一文多发平台 OpenWrite 发布!
-
从零开始学习贪心算法12-26
-
线性模型入门教程:基础概念与实践指南12-26
-
探索随机贪心算法:从入门到初级应用12-25
-
树形模型进阶:从入门到初级应用教程12-25
-
搜索算法进阶:新手入门教程12-25
-
算法高级进阶:新手与初级用户指南12-25
-
随机贪心算法进阶:初学者的详细指南12-25
-
贪心算法进阶:从入门到实践12-25
-
线性模型进阶:初学者的全面指南12-25
-
朴素贪心算法教程:初学者指南12-25
-
树形模型教程:从零开始的图形建模入门指南12-25
-
搜索算法教程:初学者必备指南12-25
-
算法高级教程:入门与初级用户指南12-25
-
随机贪心算法教程:初学者指南12-25
-
贪心算法教程:入门与实践指南12-25