一、简介

Apriori算法是一种用于挖掘数据集中频繁项集的算法，进而用于生成关联规则。这种算法在数据挖掘、机器学习、市场篮子分析等多个领域都有广泛的应用。

什么是关联规则挖掘？

关联规则挖掘是数据挖掘中的一个重要分支，其目标是发现在一个数据集中变量间存在的有趣的关联或模式。

例子： 假设在一个零售商的交易数据中，如果客户购买了啤酒，他们也很有可能购买薯片。这里的“啤酒”和“薯片”就形成了一个关联规则。

什么是频繁项集？

频繁项集是在数据集中出现次数大于或等于最小支持度（Minimum Support Threshold）的项的集合。

例子： 在超市购物数据中，如果“牛奶”和“面包”这一组合经常一起出现在同一个购物篮里，并且出现的次数超过了最小支持度，那么{“牛奶”, “面包”}就是一个频繁项集。

什么是支持度与置信度？

• 支持度（Support）: 是某个项集在所有交易中出现的频率。它用于衡量一个项集的普遍性。

  例子： 如果我们有100笔交易，其中有30笔交易包含了“牛奶”，那么“牛奶”的支持度就是30%。

• 置信度（Confidence）: 是在A出现的情况下，B出现的条件概率。

  例子： 如果在包含“牛奶”的所有交易中，有70%的交易也包含了“面包”，那么从“牛奶”到“面包”的置信度就是70%。

Apriori算法的重要性

Apriori算法由于其简单、高效的特性，在数据挖掘中有着广泛的应用。它不仅能用于挖掘数据中的隐藏模式，还能用于诸如产品推荐、用户行为分析、网络安全等多个应用场景。

例子： 在电子商务网站中，Apriori算法可以用于分析用户购买历史数据，进而实现个性化推荐，提升销售额和用户满意度。

应用场景

由于其广泛的用途和灵活性，Apriori算法在以下几个主要领域内有着广泛的应用：

• 市场篮子分析: 了解哪些产品经常被一起购买，以进行有效的产品布局或优惠策略。

• 医疗诊断: 分析病人的历史数据，找出病症和治疗方案之间的关联。

• 网络安全: 通过分析网络日志，找出异常模式，以预防或检测安全威胁。

通过这些定义和例子，我们可以更全面地了解Apriori算法的基本概念、重要性和应用范围，为后续的技术解析和实战应用打下坚实的基础。

二、理论基础

在深入探讨Apriori算法之前，理解其背后的理论基础是非常重要的。本节将详细介绍关联规则挖掘的基础概念，包括项集、支持度、置信度、提升度以及如何使用这些概念来挖掘有用的关联规则。

项和项集

• 项（Item）: 在关联规则挖掘中，项通常指数据集中的一个元素。

  例子： 在一个超市的购物篮数据中，“牛奶”、“面包”、"啤酒"等都是单个的项。

• 项集（Itemset）: 是一个项的集合，可以包含一个或多个项。

  例子： {“牛奶”, “面包”} 和 {“啤酒”, “薯片”, “面包”} 都是项集。

支持度（Support）

支持度是一个度量，用于表示一个项集在整个数据集中出现的频率。

!file

置信度（Confidence）

置信度表示在包含项集X的所有事务中，也包含项集Y的事务的概率。

提升度（Lift）

提升度用于衡量项集X和Y的出现是否相互独立。

Apriori原理

Apriori原理是Apriori算法的核心，它基于一个简单但重要的观察：一个项集是频繁的，那么它的所有子集也必须是频繁的。

例子： 如果{“牛奶”, “面包”, “啤酒”}是一个频繁项集，那么{“牛奶”, “面包”}、{“牛奶”, “啤酒”}和{“面包”, “啤酒”}也必须是频繁项集。

通过以上的概念和例子，我们应该对关联规则挖掘的基础理论有了更深入的了解。这为我们后续详解Apriori算法以及实际应用提供了坚实的基础。

三、Apriori算法概述

Apriori算法是由Agrawal和Srikant于1994年提出的，用于高效地挖掘频繁项集和生成关联规则。其名字“Apriori”来源于拉丁语，意为“从先验知识”。这很好地反映了算法的核心思想：利用已知的频繁项集（即先验知识）来更有效地找到更大的频繁项集。

算法步骤

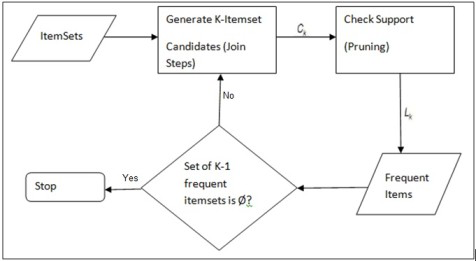
Apriori算法的执行流程主要包含两个步骤：

1. 频繁项集生成（Frequent Itemset Generation）: 找出满足最小支持度阈值的所有频繁项集。

2. 关联规则生成（Association Rule Generation）: 从频繁项集中生成高置信度的关联规则。

频繁项集生成

1. 扫描数据集，找出所有单一项的支持度，并筛选出满足最小支持度的项。
2. 使用满足最小支持度的项生成新的候选项集。
3. 计算新生成的候选项集的支持度，并再次筛选。
4. 重复上述步骤，直到不能生成新的频繁项集。

例子： 假设有一个购物交易数据集，其中包括5笔交易。第一步是计算所有单一商品（如“牛奶”，“面包”等）在这5笔交易中的出现次数，并筛选出那些出现次数达到最小支持度的商品。

关联规则生成

1. 对于每一个频繁项集，生成所有可能的非空子集。
2. 对每一条生成的规则 ( A \Rightarrow B )，计算其置信度。
3. 如果规则的置信度满足最小置信度要求，则该规则为有效关联规则。

例子： 对于频繁项集 {“牛奶”, “面包”, “黄油”}，可能的规则有 “牛奶, 面包 -> 黄油”, “牛奶, 黄油 -> 面包” 等。计算这些规则的置信度，并筛选出满足最小置信度的规则。

优缺点

优点

• 简单易懂: Apriori算法基于直观的原理，并且计算过程简单。
• 可扩展性强: 算法可以应用于大规模的数据集。

缺点

• 计算量大: 在大数据集上，可能需要生成大量的候选项集。
• 多次扫描数据: 算法需要多次扫描数据集以计算项集的支持度，这在数据集很大时可能是低效的。

例子： 在一个包含百万级交易数据的电子商务网站中，使用Apriori算法可能需要消耗大量计算资源和时间。

通过以上的详细描述和例子，我们应该对Apriori算法有了全面而深入的理解。这为我们后续的技术解析和实战应用奠定了基础。

四、实战应用

在理解了Apriori算法的理论基础和工作原理之后，现在我们将进一步探讨其在实际场景中的应用。特别是在购物篮分析和推荐系统中，Apriori算法被广泛应用。

为了更好地说明这一点，下面将通过Python展示如何实现Apriori算法，并用一个简单的购物数据集进行演示。

购物篮分析

购物篮分析（Market Basket Analysis）是一种在零售业非常流行的技术，用于发现顾客购买产品之间的关联规则。

输入和输出

• 输入： 一组交易数据，每一笔交易包含多个购买的商品。
• 输出： 满足最小支持度和最小置信度的关联规则。

Python实现代码

首先导入必要的库：

from itertools import chain, combinations

接着定义几个辅助函数：

# 生成候选项集的所有非空子集
def powerset(s):
    return chain.from_iterable(combinations(s, r) for r in range(1, len(s)))

# 计算支持度
def calculate_support(itemset, transactions):
    return sum(1 for transaction in transactions if itemset.issubset(transaction)) / len(transactions)

现在我们来实现Apriori算法：

def apriori(transactions, min_support, min_confidence):
    # 初始化频繁项集和关联规则列表
    frequent_itemsets = []
    association_rules = []
    
    # 第一步：找出单项频繁项集
    singletons = {frozenset([item]) for transaction in transactions for item in transaction}
    singletons = {itemset for itemset in singletons if calculate_support(itemset, transactions) >= min_support}
    frequent_itemsets.extend(singletons)
    
    # 迭代找出所有其他频繁项集
    prev_frequent_itemsets = singletons
    while prev_frequent_itemsets:
        # 生成新的候选项集
        candidates = {itemset1 | itemset2 for itemset1 in prev_frequent_itemsets for itemset2 in prev_frequent_itemsets if len(itemset1 | itemset2) == len(itemset1) + 1}
        
        # 计算支持度并筛选
        new_frequent_itemsets = {itemset for itemset in candidates if calculate_support(itemset, transactions) >= min_support}
        frequent_itemsets.extend(new_frequent_itemsets)
        
        # 生成关联规则
        for itemset in new_frequent_itemsets:
            for subset in powerset(itemset):
                subset = frozenset(subset)
                diff = itemset - subset
                if diff:
                    confidence = calculate_support(itemset, transactions) / calculate_support(subset, transactions)
                    if confidence >= min_confidence:
                        association_rules.append((subset, diff, confidence))
                        
        prev_frequent_itemsets = new_frequent_itemsets

    return frequent_itemsets, association_rules

示例和输出

假设我们有以下简单的购物数据集：

transactions = [
    {'牛奶', '面包', '黄油'},
    {'啤酒', '面包'},
    {'牛奶', '啤酒', '黄油'},
    {'牛奶', '鸡蛋'},
    {'面包', '鸡蛋', '黄油'}
]

调用Apriori算法：

min_support = 0.4
min_confidence = 0.5

frequent_itemsets, association_rules = apriori(transactions, min_support, min_confidence)

print("频繁项集：", frequent_itemsets)
print("关联规则：", association_rules)

输出可能如下：

频繁项集： [{'牛奶'}, {'面包'}, {'黄油'}, {'啤酒'}, {'鸡蛋'}, {'牛奶', '面包'}, {'牛奶', '黄油'}, {'面包', '黄油'}, {'啤酒', '黄油'}, {'面包', '啤酒'}]
关联规则： [(('牛奶',), ('面包',), 0.6666666666666666), (('面包',), ('牛奶',), 0.6666666666666666), ...]

通过这个实战应用，我们不仅学习了如何在Python中实现Apriori算法，还了解了它在购物篮分析中的具体应用。这为进一步的研究和实际应用提供了有用的指导。

五、性能优化与扩展

Apriori算法虽然在多个领域有着广泛的应用，但其在大数据集上的性能表现并不尽如人意。这是由于它需要多次扫描数据集以及生成大量的候选项集。在这一节中，我们将讨论针对这些问题的性能优化方案和扩展方法。

优化策略

优化Apriori算法的主要方法包括：

减少数据扫描次数

由于Apriori算法在每一轮都需要扫描整个数据集以计算支持度，因此一个直观的优化方式就是减少数据扫描的次数。

例子： 通过构建一个事务-项倒排索引，你可以在单次数据集扫描后立即找到任何项集的支持度。

采用数据压缩技术

可以通过压缩事务数据来减少计算量，例如使用位向量来表示事务。

例子： 若数据集中有100个商品，每一笔交易都可以通过一个100位的位向量来表示。这种方式可以显著减少数据的存储需求。

使用Hashing技术

通过使用哈希表来存储候选项集和它们的计数，可以加速支持度的计算。

例子： 在生成候选项集时，可以使用哈希函数来将项集映射到哈希表的一个位置，并在该位置增加相应的计数。

扩展方法

并行化

Apriori算法可以通过数据或任务并行化进行扩展，以利用多处理器或分布式计算环境。

例子： 在一个分布式系统中，可以将数据集划分为多个子集，并在各个节点上并行计算支持度和生成频繁项集。

支持近似挖掘

对于一些应用场景，完全精确的频繁项集挖掘可能不是必需的。在这种情况下，可以使用近似算法来加速计算。

例子： 使用Monte Carlo方法或其他随机抽样技术，通过部分数据来估计整个数据集的频繁项集。

集成其他数据挖掘算法

Apriori算法可以与其他数据挖掘或机器学习算法结合使用，以解决更复杂的问题。

例子： 在一个推荐系统中，除了使用Apriori算法找出频繁项集外，还可以使用聚类算法对用户进行分群，从而实现更个性化的推荐。

通过这些优化和扩展方法，我们不仅可以提升Apriori算法在大数据环境下的性能，还可以拓宽其应用范围。这些都为进一步的研究和应用提供了有益的方向。

六、总结

通过本文的探讨，我们不仅对Apriori算法有了全面且深入的了解，而且掌握了它在实际问题中的应用，特别是在购物篮分析和推荐系统方面。然而，我们也注意到了这一算法在面对大规模数据时存在的局限性。

技术洞见

• 支持度与置信度的平衡： 在实际应用中，选择合适的支持度和置信度阈值是一门艺术。过低的阈值可能会导致大量不显著的关联规则，而过高的阈值可能会漏掉一些有用的规则。

• 实时性问题： 在动态变化的数据集上，如何实现Apriori算法的实时或近实时分析也是一个值得关注的问题。这在电子商务等快速响应的场景中尤为重要。

• 多维、多层分析： 现有的Apriori算法主要集中在单一的项集层面，未来可以考虑如何将其扩展到多维或多层的关联规则挖掘。

• 算法与模型的集成： 未来的研究趋势可能会更多地集中在将关联规则挖掘与其他机器学习模型（如神经网络、决策树等）集成，以解决更为复杂的问题。

在今后的工作中，探究这些技术洞见的相关性和应用价值，以及将Apriori算法与现代计算架构（如GPU、分布式计算等）更紧密地结合，将是关键的研究方向。

总之，Apriori算法在数据挖掘和关联分析领域有着广阔的应用前景。然而，为了使其能够更好地适应现代数据的规模和复杂性，还需要在算法优化和应用扩展方面进行更多的研究和探索。希望本文能为您在这一领域的学习和应用提供有用的信息和启示。