8

要求

时间限制：3秒 空间限制：32768K

题目描述

把一个数组最开始的若干个元素搬到数组的末尾，我们称之为数组的旋转。 输入一个非递减排序的数组的一个旋转，输出旋转数组的最小元素。 例如数组{3,4,5,1,2}为{1,2,3,4,5}的一个旋转，该数组的最小值为1。 NOTE：给出的所有元素都大于0，若数组大小为0，请返回0。

解题思路

首先对数组进行观察，发现最小的那个数一定在两个子数组的交界处。并且左边的子数组一定比右边的子数组要大

根据上面找到的性质，可以简单的想到顺序搜索，找出它们交界处即可；但是时间复杂度为O(n)

如果要求时间复杂度更低，这里可以采用二分查找法，这样时间复杂度就可以变成O(logn)

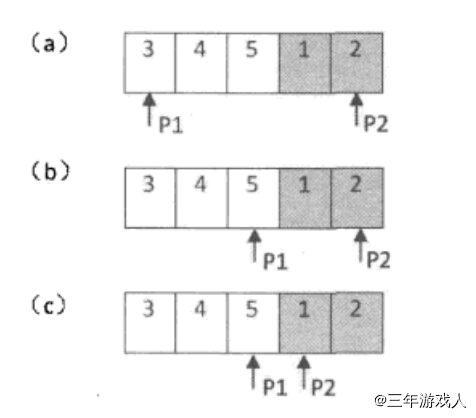
算法执行过程如下图所示：

这道题还要考虑一些特殊情况：

1. $a[P1]==a[mid]==a[P2]$，如下图所示

2. 数组本身就是排好序的，没有旋转也算是一种旋转

3. 数组只有一个数字的情况

C++代码

class Solution {
public:
  int minNumberInRotateArray(vector<int> rotateArray) {
  int size = rotateArray.size();
    if(size == 0){
      return 0;
    }
    
    int leftIdx = 0;
    int rightIdx = size - 1;
    //特殊情况，没有旋转
    if(rotateArray[leftIdx] < rotateArray[rightIdx])
      return rotateArray[leftIdx];
    
    int midIdx=0;
    while(rightIdx - leftIdx != 1){
      midIdx = (leftIdx + rightIdx) / 2;
      if(rotateArray[leftIdx] == rotateArray[midIdx] && rotateArray[midIdx] == rotateArray[rightIdx]){
        //直接用顺序查找
        return orderSearch(rotateArray, leftIdx, rightIdx);
      }
      else if(rotateArray[midIdx] > rotateArray[rightIdx]){
        leftIdx = midIdx;
      }
      else if(rotateArray[leftIdx] > rotateArray[midIdx]){
        rightIdx = midIdx;
      }
    }
    
    return rotateArray[rightIdx];
  }
  
  int orderSearch(vector<int> &rotateArray, int leftIdx, int rightIdx){
    int minVal=rotateArray[leftIdx];
    for(int i = leftIdx + 1;i <= rightIdx;++i){
      if(rotateArray[i] < minVal)
        minVal=rotateArray[i];
    }
    return minVal;
  }
};