一，简单的递归（求阶乘）

阶乘： n!=1×2×3×…×(n-1)×n

// 例如：求5的阶乘是：1×2×3×4×5
function factorial(n){
   if( n<1 ) return
   return n*factorial(n-1)
}

 console.log(factorial(5)) // 120

二，递归函数的调用顺序

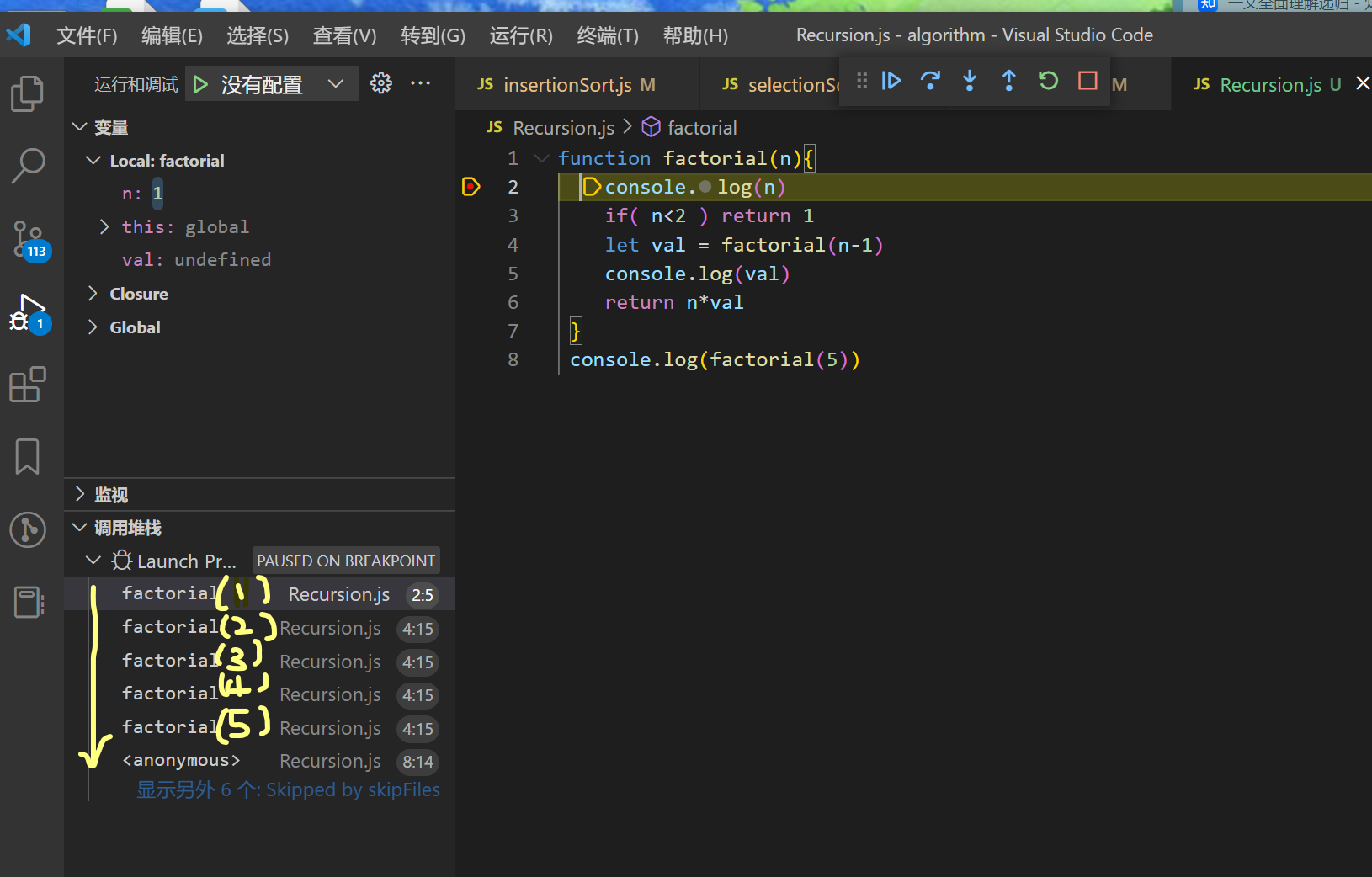
function factorial(n){
    console.log(n)
    if( n<2 ) return 1
    let val = factorial(n-1)
    console.log(val) 
    return n*val
 }

factorial(5) // 输出: 5,4,3,2,1,1,2,6,24,120

三，解决困惑

1.理解栈结构（后进先出）

这个弹夹相对于子弹来说，是栈结构，因为子弹是后进先出的，我们下面把函数当作子弹。

2.借助开发工具来打断点

1）打开vscode ，输入上面的案例代码，然后打上断点，然后按下 f5 ， 通过 “单步调试（f11）”，我们可以看到左侧的调用堆栈在不断的被推入

3.什么时候入栈，什么时候出栈？

1.函数没有 return 的时候，调用了新的函数，就会入栈，return就会出栈。所以 打印入参 是 5，4，3，2，1 。因为这几个入参 都大于等于2 ，所以会走到 第四行，因为是在return之前，所以会入栈。

四，总结

1.理解的函数 的调用堆栈，复杂的递归也可以理解了。 通过第三个部分的方法 ，举一反三，来试着理解下面的代码（归并排序）,通过画图的方式去理解效果会更好。

Array.prototype.mergeSort = function () {
  const rec = (arr) => {
    if (arr.length === 1) { // 调用堆栈 出栈
      return arr;
    }
    const mid = arr.length >> 1

    const l = arr.slice(0, mid);
    const r = arr.slice(mid, arr.length);

    console.log(l,r)

    const L = rec(l); // 调用堆栈 入栈
    const R = rec(r); // 调用堆栈 入栈

    const res = [];

    while (L.length || R.length) {
      L.length && R.length
        ? L[0] < R[0]
          ? res.push(L.shift())
          : res.push(R.shift())
        : L.length
        ? res.push(L.shift())
        : res.push(R.shift());
    }
    console.log(res)
    return res;
  };
  const res = rec(this);
  res.forEach((n, i) => {
    this[i] = n;
  });
};

const arr = [11,10,8,7,3];
arr.mergeSort();