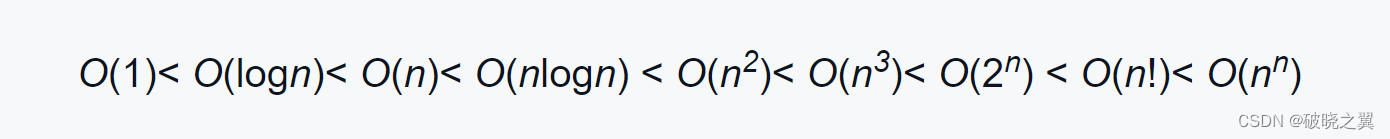Java教程
【金秋打卡】第2天 JavaScript版数据结构与算法-时间/空间复杂度计算
课程名称:JavaScript版数据结构与算法
课程章节:时间/空间复杂度计算
课程讲师: lewis
课程内容:
课程介绍
时间复杂度计算
空间复杂度计算
个人是从软件二次开发开始学习系统学习程序开发的,之前的要求是能跑,但是现在到产品岗后,日常工作中也需要找到性能瓶颈,除去网络延时,服务器CPU,内存大小,硬盘I/O,SQL执行效率等,程序的算法也是一个重要的指标,需要对其有足够的认识,
一 、 算法的时间性能分析
(1)算法耗费的时间和语句频度
一个算法所耗费的时间=算法中每条语句的执行时间之和。
每条语句的执行时间=语句的执行次数(即频度(Frequency Count))×语句执行一次所需时间。
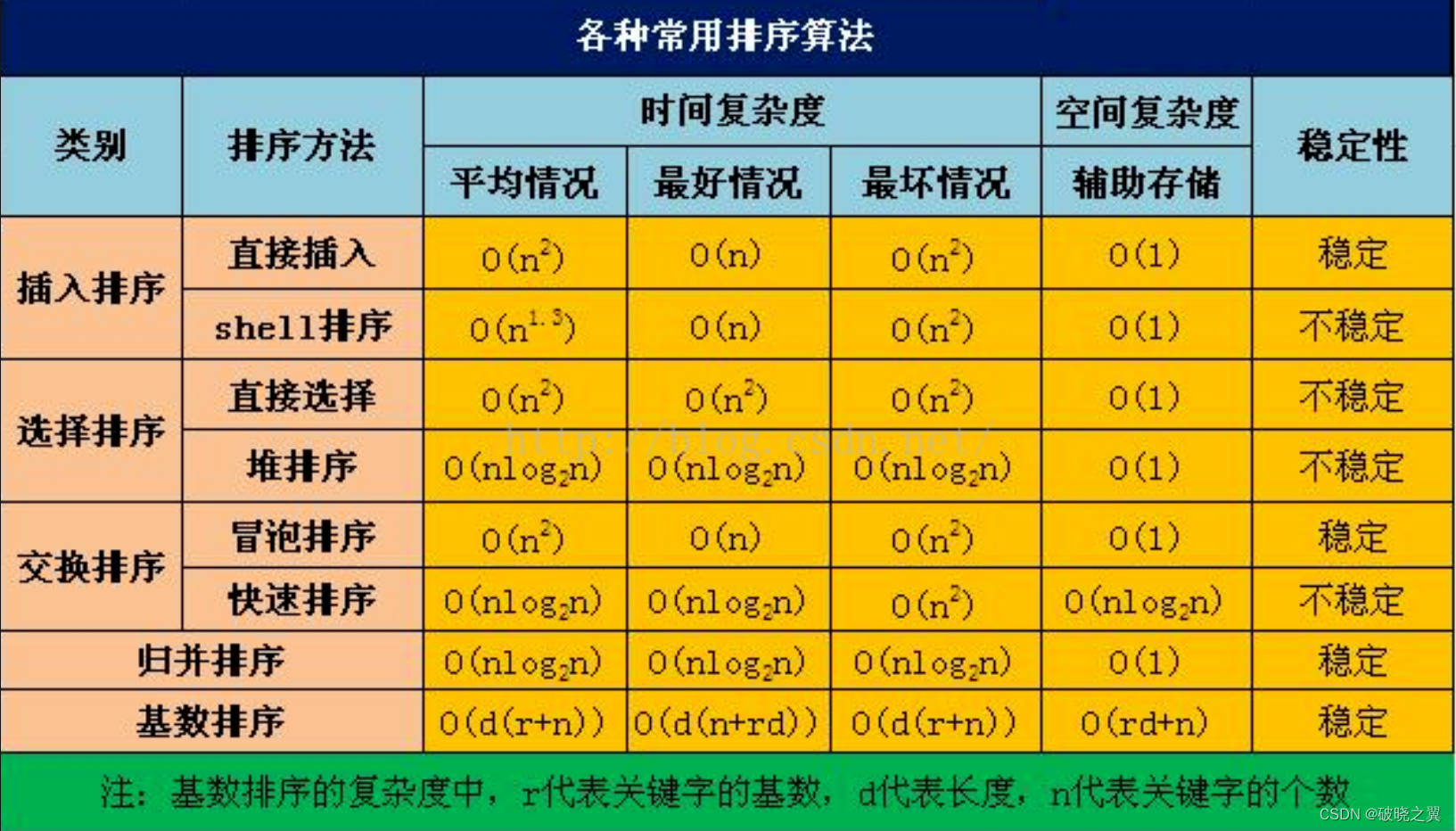
时间复杂度有一些评价标准:
首先声明算法效率的排序方式,从小到大依次如下:
运行效率排序:
常数阶O(1)>对数阶O(logN)>线性阶O(n)>线性对数阶O(nlogN)>平方阶O(n²)>立方阶O(n³)>指数阶(2^n)> 阶乘O(n!) >循环递归O(n^n)
-
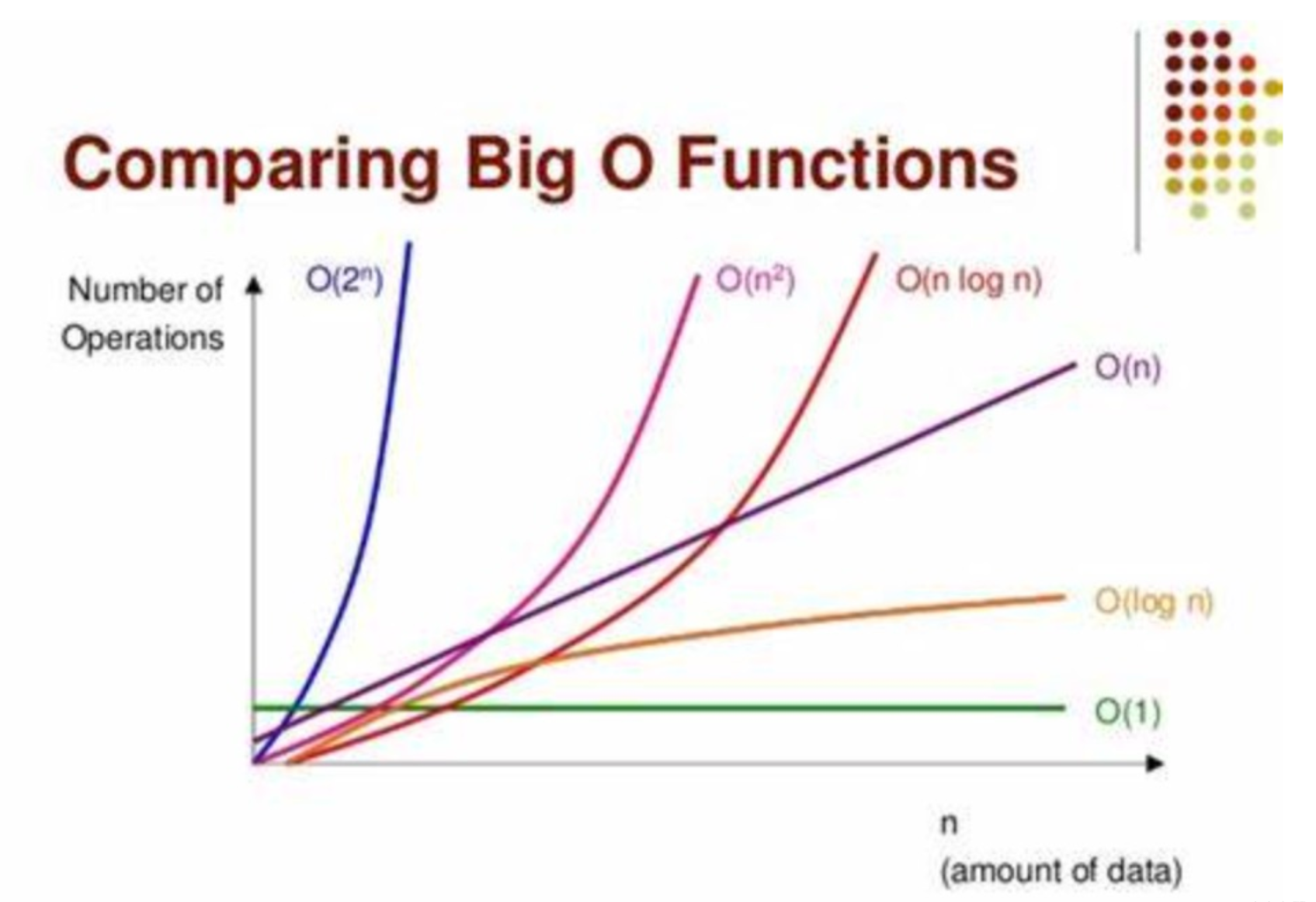
符合常数型函数曲线特性的算法
最好的时间复杂度就是O(1),O(1)表示在一个常数时间,并且是只要一条语句就能执行完的功能,它的时间开销是就O(1)常数时间是一条直线,你的元素规模不管是1个、2个、3个、4个、还是100个、1000个它所需要的时间都是恒定的如果程序达不到O(1)的性能,但能达到一个常数级别O(2)、O(3)、O(4)、O(5)也是很好的,也就是说你不管程序的规模怎么样,只要固定的只需要一条、两条、三条、四条或者五条语句,或者是固定的语句数量就能完成, -
符合对数性函数曲线特性的算法
差一点的情况是O(logn),它是一条弧线,当元素个数增加时,算法的程序性能消耗并没有快速地增加,而是增加的速度越来越缓慢,这种程序性能也不错再差一点就是一条斜线,什么意思?随着元素个数的增加,运算时间也增加,这种就没有O(logn)好,因为O(logn)是元素越多,时间开销反而增加的没那么厉害,线性时间还会增加。 -
符合指数型函数曲线特性的算法
那比较不好的是什么呢?就是O(n)的平方,大家还记得中学里学过的O(n)的平方是一条什么样的曲线吗?它是一条开口朝上的抛物线,这个抛物线就是随着你的程序规模增加,程序的运行时间会显著的增加,这就非常不好了为什么?因为它就意味着你的程序,在元素个数少的时候跑得比较快,元素个数越多跑得就越慢那如果是n的三次方呢?那就更糟糕了,五次方、十次方也一样,这就是我们衡量性能的标准
用最直白的话来说:一般开发应用中看:循环嵌套几层,每一层的循环次数和哪个变量有关?
二、 空间复杂度
空间复杂度就看你申请内存用了多少(数组长度),与哪个变量有关O(),logn中对数函数的底数是多少一般来说是 222 。因为计算机中很多地方采用的是二分法。
当然,如果非要三分、四分法解决问题,那么底数就相应变成3、4但是,其实 O(log2n)=O(log3n/log23)=O(log3n)O(log_2n)=O(log_3n/log_23)=O(log_3n)O(log_2n)=O(log_3n/log_23)=O(log_3n)
(常数可以扔掉),所以你爱写啥都随便。
三、课程收获
对程序的算法设计对性能的影响有了比较直观的了解。
-
数据结构与算法面试题详解及练习12-27
-
网络请求面试题详解与实战12-27
-
数据结构和算法面试真题详解与实战教程12-27
-
网络请求面试真题解析与实战教程12-27
-
数据结构和算法大厂面试真题详解与实战指南12-27
-
TS大厂面试真题解析与应对策略12-27
-
TS大厂面试真题详解与解析12-27
-
网站安全入门:如何识别和修复漏洞12-27
-
SQL注入基础教程12-27
-
初学者指南:理解和修复跨域漏洞12-27
-
SQL注入基础知识详解与防范方法12-27
-
SQL注入学习:初学者指南12-27
-
SQL注入学习:初学者指南12-27
-
数据库服务漏洞入门:新手必读指南12-27
-
SQL注入入门:新手必读教程12-27