Python教程
【九月打卡】第21天 Python3入门机器学习
本文主要是介绍【九月打卡】第21天 Python3入门机器学习,对大家解决编程问题具有一定的参考价值,需要的程序猿们随着小编来一起学习吧!
①课程介绍
课程名称:Python3入门机器学习 经典算法与应用 入行人工智能
课程章节:11-1;11-2;11-3;11-4
主讲老师:liuyubobobo
内容导读
- 第一部分 SVM中使用多项式特征
- 第二部分 使用多项式核函数的SVM
- 第三部分 SVM思想解决回归问题
②课程详细
第一部分 SVM中使用多项式特征
导入函数
import numpy as np import matplotlib.pyplot as plt
创建X,y
from sklearn import datasets X, y = datasets.make_moons()
可视化创建的数据
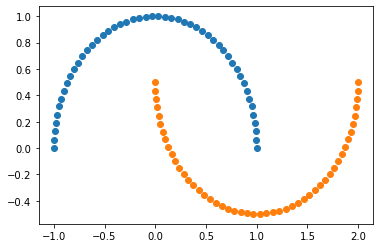
plt.scatter(X[y==0,0], X[y==0,1]) plt.scatter(X[y==1,0], X[y==1,1]) plt.show()
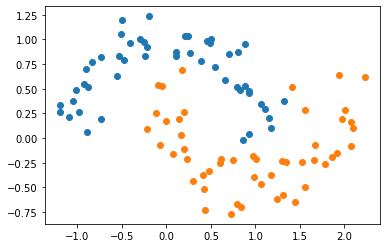
#增加扰动 X, y = datasets.make_moons(noise=0.15,random_state=666)
plt.scatter(X[y==0,0], X[y==0,1]) plt.scatter(X[y==1,0], X[y==1,1]) plt.show()
接下来我们加入使用普通的SVM则难以得到合适的决策边界,应为SVM原则上只能使用线性的决策边界,像这种弯曲的决策边界,则需要使用多项式特征的SVM具体使用办法,和多项式线性回归很相似
创建管道符,放入多项式,归一化,SVC
from sklearn.preprocessing import PolynomialFeatures, StandardScaler
from sklearn.svm import LinearSVC
from sklearn.pipeline import Pipeline
def PolynomialSVC(degree,C=0.1):
return Pipeline([
('Poly',PolynomialFeatures(degree=degree)),
('standard',StandardScaler()),
('linearSVC',LinearSVC(C=C))
])
调用方式和以前的差不多
poly= PolynomialFeatures(degree=2) poly.fit(X) X_re = poly.transform(X)
定义决策边界可视化函数
def plot_decision_boundary(model, axis):
x0, x1 = np.meshgrid(
np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
)
X_new = np.c_[x0.ravel(), x1.ravel()]
y_predict = model.predict(X_new)
zz = y_predict.reshape(x0.shape)
from matplotlib.colors import ListedColormap
custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
可视化
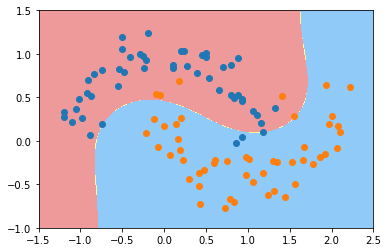
plot_decision_boundary(poly_svc, axis=[-1.5, 2.5, -1.0, 1.5]) plt.scatter(X[y==0,0],X[y==0,1]) plt.scatter(X[y==1,0],X[y==1,1]) plt.show()
第二部分 使用多项式核函数的SVM
对数据进行处理能得到非线性的决策边界,还有第二种办法能得到非线性决策边界——多项式核函数
调用方法SVC中填入核函数,高斯核函数,或者多项式核函数
from sklearn.svm import SVC
def PolynomialKernelSVC(degree,C=1.0):
return Pipeline([
('standard',StandardScaler()),
('linearSVC',SVC(kernel='poly',C=C,degree=degree))
])
进行调用查看效果
poly_kernel_svc = PolynomialKernelSVC(degree=3) poly_kernel_svc.fit(X,y)
可视化多项式核函数决策边界
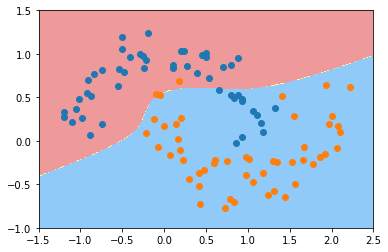
plot_decision_boundary(poly_kernel_svc, axis=[-1.5, 2.5, -1.0, 1.5]) plt.scatter(X[y==0,0],X[y==0,1]) plt.scatter(X[y==1,0],X[y==1,1]) plt.show()
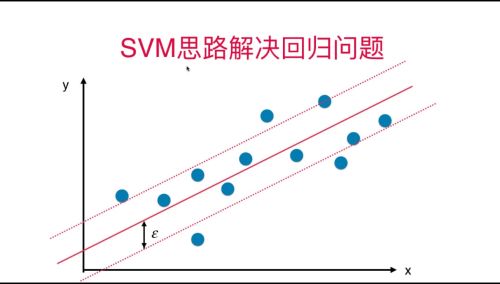
第三部分 SVM思想解决回归问题
我们如何用SVM来决绝回归问题
SVM思想解决回归问题
SVM线性回归问题基本理念:在margin中数据点越多与好(SVM分类问题相反)
超参数:epsilon
import numpy as np import matplotlib.pyplot as plt
导入数据
from sklearn import datasets boston = datasets.load_boston() X = boston.data y = boston.target
对数据进行分割
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
创建管道符使用线性回归
from sklearn.svm import LinearSVR
from sklearn.svm import SVR
from sklearn.preprocessing import StandardScaler
from sklearn.pipeline import Pipeline
def StandardLinearSVR(epsilon=0.1):
return Pipeline([
('std',StandardScaler()),
('linearSVR',LinearSVR(epsilon=epsilon))
])
按照以前的方法进行调用
svr = StandardLinearSVR() svr.fit(X_train, y_train)
svr.score(X_test,y_test)
③课程思考
- SVC可以导入核函数(高斯核函数,多项式核函数)嫩解决分类问题
- LinearSVR可以解决线性回归的问题,
- LinearSVC线性SVC,和数据多项式化,也可以实现核函数类似的效果
- 据我观察,多项式特征(或者多项式核)和高斯核都是在做升维,只是升维的方式不同。
④课程截图
这篇关于【九月打卡】第21天 Python3入门机器学习的文章就介绍到这儿,希望我们推荐的文章对大家有所帮助,也希望大家多多支持为之网!
您可能喜欢
-
Python编程基础教程12-27
-
Python编程基础指南12-27
-
Python编程入门指南12-24
-
Python编程基础入门12-24
-
Python编程基础:变量与数据类型12-24
-
使用python部署一个usdt合约,部署自己的usdt稳定币12-23
-
Python编程入门指南12-20
-
Python编程基础与进阶12-20
-
Python基础编程教程12-19
-
python 文件的后缀名是什么 怎么运行一个python文件?-icode9专业技术文章分享12-19
-
使用python 把docx转为pdf文件有哪些方法?-icode9专业技术文章分享12-19
-
python怎么更换换pip的源镜像?-icode9专业技术文章分享12-19
-
Python资料:新手入门的全面指南12-19
-
Python股票自动化交易实战入门教程12-19
-
Python股票自动化交易入门教程12-19
栏目导航