Python教程
【九月打卡】第19天 Python3入门机器学习
本文主要是介绍【九月打卡】第19天 Python3入门机器学习,对大家解决编程问题具有一定的参考价值,需要的程序猿们随着小编来一起学习吧!
①课程介绍
课程名称:Python3入门机器学习 经典算法与应用 入行人工智能
课程章节:10-2;10-3;10-4
主讲老师:liuyubobobo
内容导读
- 第一部分 精准率和召回率
- 第二部分 实现混淆矩阵,精准率和召回率
- 第三部分 实现F1 score
- 第四部分
②课程详细
第一部分 精准率和召回率
有时候数据极端的话,对于分类问题的分类情况很糟糕,很难衡量,比如癌症病人10000个人里有一个,我只要是算法恒等于1,就能拿到99.99%的准确率,但却并不可信,这时候就要引入精准率和召回率
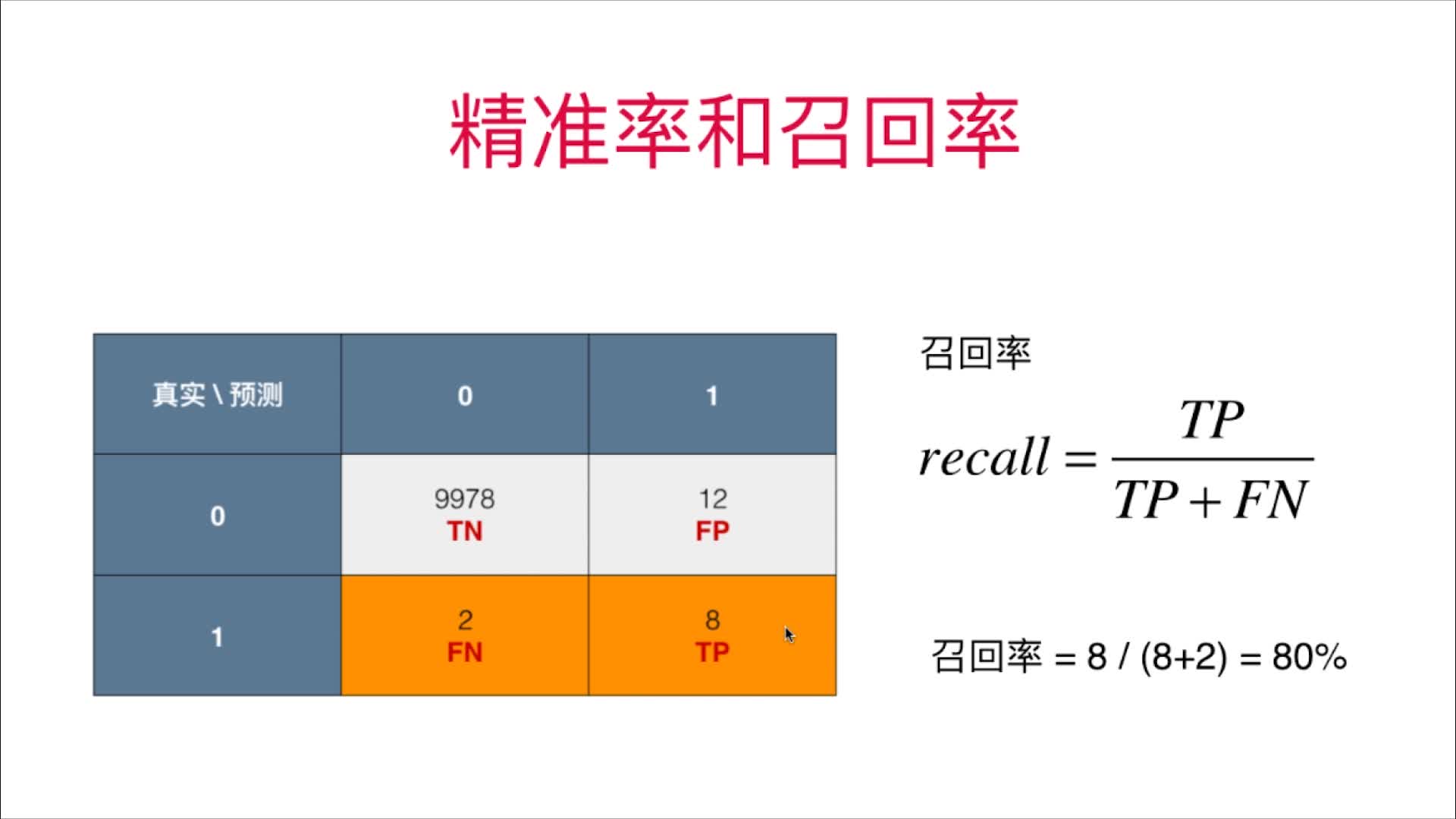
召回率:我们关注的事件真实的发生了,真实发生了的数据中,我们成功预测了多少
(实际上有100个我们关注的事件发生,其中有多少个是准确的)
在极其有偏的数据中,我们不看分类准确度,只看精准率和召回率,才可以更好的评价分类模型的好坏
第二部分 实现混淆矩阵,精准率和召回率
导入函数
import numpy as np from sklearn import datasets
将数据变成二分类问题
digits = datasets.load_digits() X = digits.data y = digits.target.copy() y[digits.target==9] = 1 y[digits.target!=9] = 0
进行数据分割
from sklearn.model_selection import train_test_split X_train, X_test, y_train, y_test = train_test_split(X, y, random_state=666)
带入逻辑回归
from sklearn.linear_model import LogisticRegression log_reg = LogisticRegression() log_reg.fit(X_train, y_train)
定义混淆矩阵,精准率,和召回率的函数
def TN(y_true, y_predict):
assert len(y_true) == len(y_predict)
return np.sum(y_test_predict[y_test == 0] ==0)
def FN(y_true, y_predict):
assert len(y_true) == len(y_predict)
return np.sum(y_test_predict[y_test == 1] ==0)
def FP(y_true, y_predict):
assert len(y_true) == len(y_predict)
return np.sum(y_test_predict[y_test == 0] ==1)
def TP(y_true, y_predict):
assert len(y_true) == len(y_predict)
return np.sum(y_test_predict[y_test == 1] ==1)
混淆矩阵
def confusion_matrix(y_true, y_predict):
return np.array([
[TN(y_true, y_predict),FP(y_true, y_predict)],
[FN(y_true, y_predict),TP(y_true, y_predict)]
])
confusion_matrix(y_test, y_test_predict)
精准率与召回率
def precision(y_true, y_predict):
tp = TP(y_true, y_predict)
fp = FP(y_true, y_predict)
try:
return tp / (tp + fp)
except:
return 0.0
def recall(y_true, y_predict):
tp = TP(y_true, y_predict)
fn = FN(y_true, y_predict)
try:
return tp / (tp + fn)
except:
return 0.0
查看召回率
recall(y_test, y_test_predict)
0.8
查看精准率
precision(y_test, y_test_predict)
0.9473684210526315
第三部分 sklearn中的混淆矩阵,精准率,召回率
延续上部分代码,此部分仅仅进行调用
混淆矩阵
from sklearn.metrics import confusion_matrix confusion_matrix(y_test, y_test_predict)
准确率
from sklearn.metrics import precision_score precision_score(y_test, y_test_predict)
0.947368421052631
召回率
from sklearn.metrics import recall_score recall_score(y_test, y_test_predict)
0.8
第四部分 实现F1 score
股票预测更重视精准率(如果预测股票上升实际上下降的话会造成损失)
医疗检测更重视召回率(如果实际上患病,却预测没病。。。)
两个指标的重要性视情况而定
F1 score为precision和recall的调和平均(即使precision和recall一高一低,F1也会相对较低,因此F1兼顾了两者)
自己实现F1 score
def f1_score(precision, recall):
try:
return 2 * precision * recall / (precision + recall)
except:
return 0.0
准确率和精确率都很高,F1才会高
precision = 0.5 recall = 0.5 f1_score(precision,recall)
0.5
③课程思考
- F1 Score二者都兼顾,可以只是用这个参数很方便的
- 对于数据集极度偏斜,分类准确度评价分类算法远远不够
④课程截图
这篇关于【九月打卡】第19天 Python3入门机器学习的文章就介绍到这儿,希望我们推荐的文章对大家有所帮助,也希望大家多多支持为之网!
您可能喜欢
-
Python编程基础教程12-27
-
Python编程基础指南12-27
-
Python编程入门指南12-24
-
Python编程基础入门12-24
-
Python编程基础:变量与数据类型12-24
-
使用python部署一个usdt合约,部署自己的usdt稳定币12-23
-
Python编程入门指南12-20
-
Python编程基础与进阶12-20
-
Python基础编程教程12-19
-
python 文件的后缀名是什么 怎么运行一个python文件?-icode9专业技术文章分享12-19
-
使用python 把docx转为pdf文件有哪些方法?-icode9专业技术文章分享12-19
-
python怎么更换换pip的源镜像?-icode9专业技术文章分享12-19
-
Python资料:新手入门的全面指南12-19
-
Python股票自动化交易实战入门教程12-19
-
Python股票自动化交易入门教程12-19
栏目导航