①课程介绍

课程名称：Python3入门机器学习 经典算法与应用 入行人工智能
课程章节：9-3；9-4
主讲老师：liuyubobobo

内容导读

• 第一部分 Sigmoid函数展示
• 第二部分 逻辑回归调用
• 第三部分 逻辑回归决策边界可视化
• 第四部分 KNN算法决策边界可视化

②课程详细

第一部分 Sigmoid函数展示

导入函数

import numpy as np
import matplotlib.pyplot as plt

定义sigmoid函数

def sigmoid(t):
    return 1 / (1 + np.exp(-t))

创造数据进行可视化

x = np.linspace(-10, 10, 500)
y = sigmoid(x)

可视化

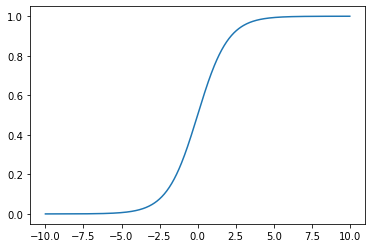
plt.plot(x, y,)
plt.show()

可以看到数据的值域被限制在了0-1，并且这种图形很适合决策

第二部分 逻辑回归调用

导入鸢尾花数据集

from sklearn import datasets

iris = datasets.load_iris()

数据调回

X = iris.data
y = iris.target
X = X[y<2]
y = y[y<2]

导入自己定义的train_test_split函数进行数据分割便于

from nike.model_selection import train_test_split

X_train, X_test, y_train, y_test = train_test_split(X_reduction, y, seed=666)

调用PCA降维到2维便于可视化与计算

from sklearn.decomposition import PCA

pca = PCA(n_components=2)
pca.fit(X_train)
X_train_reduction=pca.transform(X_train)
X_test_reduction=pca.transform(X_test)

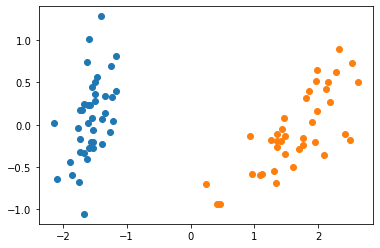
可视化降维之后的数据

plt.scatter(X_train_reduction[y_train==0,0],X_train_reduction[y_train==0,1])
plt.scatter(X_train_reduction[y_train==1,0],X_train_reduction[y_train==1,1])
plt.show()

使用逻辑回归计算准确率

from nike.LogisticRegression import LogisticRegression
log_reg = LogisticRegression()
log_reg.fit_bgd(X_train_reduction, y_train, eta=0.01)

查看准确率

log_reg.score(X_test_reduction, y_test)

1.0
可以看到准确率非常高，和数据清晰也有关

第三部分 逻辑回归决策边界可视化

找出预测的数据

y_predict_proba = log_reg.predict_proba(X_test_reduction)

定义绘制决策边界的函数

def plot_decision_boundary(model, axis):
    
    x0, x1 = np.meshgrid(
        np.linspace(axis[0], axis[1], int((axis[1]-axis[0])*100)).reshape(-1, 1),
        np.linspace(axis[2], axis[3], int((axis[3]-axis[2])*100)).reshape(-1, 1),
    )
    X_new = np.c_[x0.ravel(), x1.ravel()]

    y_predict = model.predict(X_new)
    zz = y_predict.reshape(x0.shape)

    from matplotlib.colors import ListedColormap
    custom_cmap = ListedColormap(['#EF9A9A','#FFF59D','#90CAF9'])
    
    plt.contourf(x0, x1, zz, linewidth=5, cmap=custom_cmap)
    
plot_decision_boundary(log_reg, axis=[-3, 3, -2, 2])
plt.scatter(X_train_reduction[y_train==0,0],X_train_reduction[y_train==0,1])
plt.scatter(X_train_reduction[y_train==1,0],X_train_reduction[y_train==1,1])
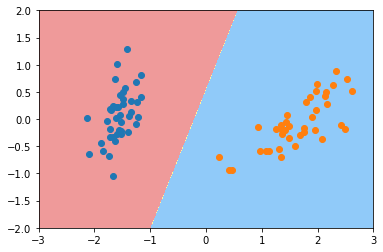
plt.show()

这个决策边界非常的合理

第四部分 KNN算法决策边界可视化

导入对象并定义

from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier()
knn_clf.fit(X_train_reduction, y_train)

KNN算法也能很好地预测数据的分布情况

knn_clf.score(X_test_reduction, y_test)

1.0
可视化，KNN算法的决策边界

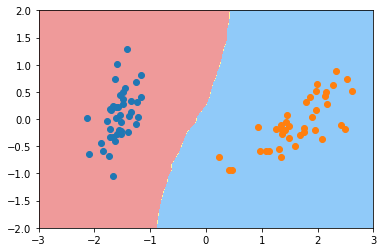
plot_decision_boundary(knn_clf, axis=[-3, 3, -2, 2])
plt.scatter(X_train_reduction[y_train==0,0],X_train_reduction[y_train==0,1])
plt.scatter(X_train_reduction[y_train==1,0],X_train_reduction[y_train==1,1])
plt.show()

有一些细微的差别，和逻辑回归来比的话

③课程思考

• 逻辑回归用一个超平面将整个空间分为两部分，对应两个类别
• 绘制决策边界的时候，将整个平面划分为均匀密铺的小点，并对不同类别使用不同的颜色

④课程截图