①课程介绍

课程名称：Python3入门机器学习 经典算法与应用 入行人工智能
课程章节：7-8;7-9;7-10;7-11
主讲老师：liuyubobobo

内容导读

• 第一部分 使用大数据MNIST进行PCA降维测试
• 第二部分 对手写字体降到二维进行可视化处理
• 第三部分 PCA降噪
• 第四部分 PCA降噪可视化

②课程详细

第一部分 使用大数据MNIST进行PCA降维测试

导入函数

import numpy as np
import matplotlib
import matplotlib.pyplot as plt
from sklearn.datasets import fetch_openml

导入数据集

mnist = fetch_openml('mnist_784')

导入数据X，y

X = mnist['data']
y = mnist['target']

这个数据集帮你分好类了，不用进行train_test_split的分割

X_train = np.array(X[:60000], dtype=float)
y_train = np.array(y[:60000], dtype=float)
X_test = np.array(X[:10000], dtype=float)
y_test = np.array(y[:10000], dtype=float)

导入knn算法

from sklearn.neighbors import KNeighborsClassifier

knn_clf = KNeighborsClassifier()
%time knn_clf.fit(X_train, y_train)

对大数据手写数据集进行预测

#很慢，
%time knn_clf.score(X_test, y_test)

CPU times: total: 1min 57s
Wall time: 49.1 s
0.9818

进行PCA降维处理

from sklearn.decomposition import PCA
pca = PCA(0.9)
pca.fit(X_train)
X_train_stand = pca.transform(X_train)
X_test_stand = pca.transform(X_test)

查看前几主成分

pca.explained_variance_ratio_

降维之后进行knn算法运行查看效率

knn_clf2 = KNeighborsClassifier()
%time knn_clf2.fit(X_train_stand, y_train)

CPU times: total: 31.2 ms
Wall time: 38.7 ms
很快
进行预测

%time knn_clf2.score(X_test_stand, y_test)

CPU times: total: 42.7 s
Wall time: 26.8 s
0.9858
快了将近1倍，

第二部分 对手写字体降到二维进行可视化处理

处理数据

np.array(X[:1]).reshape(28,28)

取出单个数据用于可视化处理

some_digit = np.array(X[1:2])

查看可视化数据是多少

y[1]

'0’
这个手写数据数据是0
接下来进行可视化看看

some_digit_image = some_digit.reshape(28, 28)
plt.imshow(some_digit_image, cmap = matplotlib.cm.binary)
plt.show()

通过可视化的手段物品们可以看出这是一个0，而我们需要机器能识别出这是0-9中的哪一个数字
接下来我们降维到三维对数据分布进行查看
降维

pca2 = PCA(n_components=3)
pca2.fit(X)
X_reduction = pca2.transform(X)

查看降维后数据的维度

X_reduction.shape

(70000, 3)

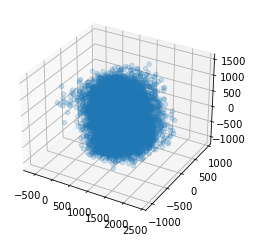
ax = plt.axes(projection='3d')
for i in range(1):
    ax.scatter3D(X_reduction[y==str(i),0], X_reduction[y==str(i),1], X_reduction[y==str(i),2], alpha=0.2)
plt.show()

数据团成一坨了，很难分清数据，准确率可能会比较低下

第三部分 PCA降噪

导入函数

import numpy as np
import matplotlib
import matplotlib.pyplot as plt

导入数据

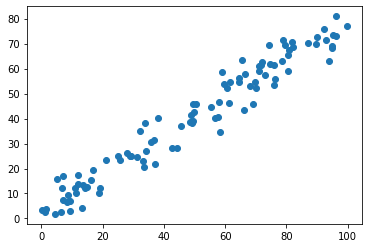
X =np.empty((100,2))
X[:,0] = np.random.uniform(0., 100., size=100)
X[:,1] = 0.75 * X[:,0] + 3 + np.random.normal(0, 5, size=100)

可视化

plt.scatter(X[:,0], X[:,1])
plt.show()

进行PCA降维然后升维查看数据分布，并进行可视化

from sklearn.decomposition import PCA
pca = PCA(n_components=1)
pca.fit(X)
X_reduction = pca.transform(X)
X_restore = pca.inverse_transform(X_reduction)

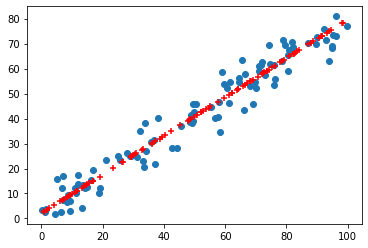
进行可视化

plt.scatter(X[:,0], X[:,1])
plt.scatter(X_restore[:,0], X_restore[:,1],color='r', marker='+')
plt.show()

第四部分 PCA降噪可视化

导入数据

from sklearn import datasets

digits = datasets.load_digits()
X = digits.data
y = digits.target

加一个正太话分布的噪音

noisy_digits = X + np.random.normal(0, 4, size=X.shape)

对可视化数据进行调整，

example_digits = noisy_digits[y==0,:][:10]
for num in range(1,10):
    example_digits = np.vstack([example_digits, noisy_digits[y==num,:][:10]])

对手写数据数据进行可视化

def plot_digits(data):
    fig, axes = plt.subplots(10, 10, figsize=(10, 10),
                             subplot_kw={'xticks':[], 'yticks':[]},
    gridspec_kw=dict(hspace=0.1, wspace=0.1)) 
    for i, ax in enumerate(axes.flat):
        ax.imshow(data[i].reshape(8, 8),
                  cmap='binary', interpolation='nearest',
                  clim=(0, 16))

    plt.show()
    
plot_digits(example_digits)

可以看到噪音还是很多的
PCA降维，在升维，发现噪音少了很多，同样也丢失了一部分数据

components = pca.transform(example_digits)
filtered_digits = pca.inverse_transform(components)
plot_digits(filtered_digits)

这个是处理之前的，数据，从可视化的角度可以看出确实，
在降维，升维的过程中丢失了一些信息
在降噪和关键信息间要选取一个平衡，视情况而定，调整

X_1 = X[y==0,:][:10]
for num in range(1,10):
    X_1= np.vstack([X_1, X[y==num,:][:10]])
    
plot_digits(X_1)

③课程思考

• 一个有意思的现象，在舍去10%的数据的信息反而准确率上升了，这说明舍去的这部分数据对最终准确率是有负相关的，也就是PCA的降噪

• 在手写字体图片识别领域，降维算法和KNN算法可以优先考虑，很适合

④课程截图