当人们提到“递归”一词，不知道如何理解它，也有人会问递归和迭代有什么区别？首先可以从定义上入手来分析，递归是自身调用自身的函数进行循环、遇到满足终止条件的情况时逐层返回来结束。迭代则是函数内某段代码实现循环，循环代码中参与运算的变量同时是保存结果的变量，当前保存的结果作为下一次循环计算的初始值。

如何实现递归算法的设计方法？

递归算法即是一种有效的算法设计方法，也是一种有效的分析问题的方法，递归算法求解问题的基本思想是：对于较为复杂的问题，把原问题分解成诺干个相对简单且类同的子问题，这样，原问题就可递推得到求解。
适宜用递归算法求解的问题的充分必要条件是：

其一，问题具有某种可借用的类同自身的子问题描述的性质：

其二，某一有限步的子问题（也称做本原问题）有直接的解存在。

如何去理解递归算法？

从小老师就教我们如何高效的从1加到100，如果我们在没有了解过高斯计数的情况下，我想大部分人，都会一个一个进行累加的方式。这样是不是得不偿失呢？那么如何描述他的代码结构呢？

"""
什么是递归？
在函数中存在着调用函数本身的情况，这种现象就叫递归。
递归思想
加入1+2+3一直加到10，如何快速的得到结果呢？
简单的可以一直加下去，采用循环的方式或者递归的方式，
其实更简单的方式是总数乘于总数加一然后除以2
推导的公式：n = n*(n+1)/2,加到100同理
"""

# 本次只做简单介绍，主要还是介绍递归思想
def recursion(num):
    if num == 1:
        return 1
    else:
        result = num + recursion(num - 1)
        return result


# 循环相加
def traverse(num):
    result = 0
    for n in range(1, num + 1):  # 第一种方案，循环添加
        result += n

从上述算法中可以看出，都可以得出结果是5050。那么不仅有小伙伴会问？这两个都可以得出相应的结果，那我在工作中，如何使用那种方案呢？
关于这一点就要去分析他们的时间复杂度和空间复杂度了。
先去计算他的时间复杂度假设时间复杂度为f(n)=2n+1, 那么f(n）的计算方法第一行执行了一个时间单位，第二行执行了n个时间单位，第三行执行了n个时间单位，可以得出f(n)=2n+1。因为时间复杂度表示的是算法随n变化的一种趋势，而f(n)=2n+1表示的就是一种线性增长关系，为了统一表达忽略常数项和系数，可得时间复杂度为O(n)！
空间复杂度是随n的变化而变化，因此空间复杂度为O(n)。

递归的算法最典型的是递归求斐波那契数列的算法

"""
递归求斐波那契数列
"""


def fibonacci(num):
    if num <= 0:
        return 0
    if num <= 1:
        return 1
    return fibonacci(num - 1) + fibonacci(num - 2)

这个求斐波那契的递归算法的时间复杂度是多少呢？
在讲解递归时间复杂度的时候，我们提到了递归算法的时间复杂度本质上是要看: 递归的次数 * 每次递归的时间复杂度。
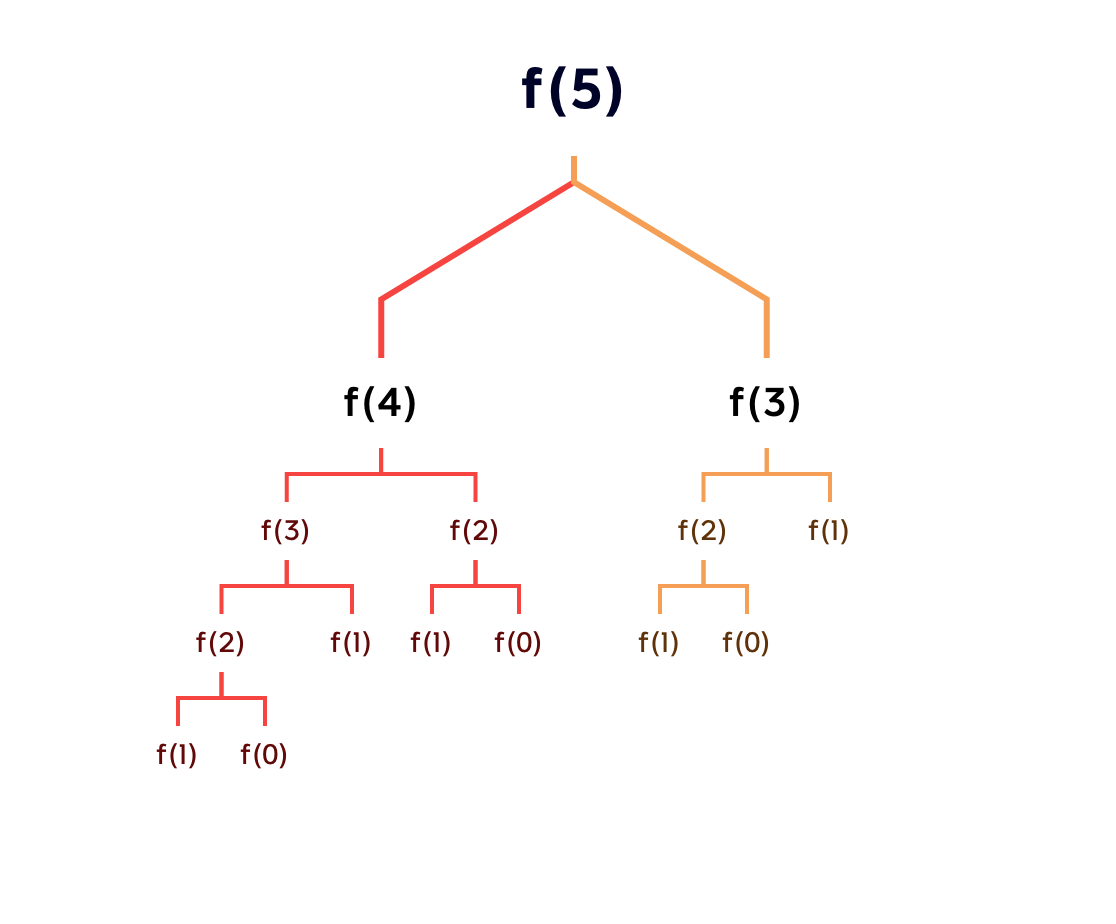
可以看出上面的代码每次递归都是O(1)的操作。再来看递归了多少次，这里将i为5作为输入的递归过程 抽象成一颗递归树，如图：

从图中，可以看出f(5)是由f(4)和f(3)相加而来，那么f(4)是由f(3)和f(2)相加而来 以此类推。
在这颗二叉树中每一个节点都是一次递归，那么这棵树有多少个节点呢？
我们之前也有说到，一棵深度（按根节点深度为1）为k的二叉树最多可以有 2^k - 1 个节点。
所以该递归算法的时间复杂度为 O(2^n) ，这个复杂度是非常大的，随着n的增大，耗时是指数上升的。

如何去理解递归算法的数据推导？

数学中经常有这样的函数，它自己定义自己。例如：n的阶乘函数f(n)=n!，n为整数：
f(n)=1 n<=1
f(n)=nf(n-1) n>1

当n小于或等于1时，f(n)的值为1，例如f(-3)=f(0)=f(1)=1。当n大于1时，f(n)是递归定义的，因为右侧也有f。但这不会导致循环完义，因为右侧f的参数小于左侧f的参数。例如，f(2)=2f(1)，因为f(1)=1，所以f(2)=21=2,以此类推，f(3)=3f(2)=32=6。
假定f(n)是直接递归的。要使函数f(n)的递归定义有一个完全的形式，需要满足如下条件：

• 有一个基础部分（base component)，它包含n的一个或多个值，对这些值，f(n)是直
  接定义的（即不用递归就能求解）。为简单起见，我们假定f的定义域是非负整数，基
  础部分包含0<=n<=k，其中k为作负常数。（n>=k的情形也是可能的，但很少见。）

• 在递归部分（recursive component），右侧f有一个参数小于n，因此重复应用递归部分可以把右侧f的表达式转变为基础部分。

总之，递归算法是程序设计中一种重要的方法，在数学和计算机科学中，使用递归的思想能解决很多运算量较大的问题，节省大量的人力资源和时间，但对于递归的概念，初学者往往感到不容易理解，那么为什么还要引入递归的概念呢？

其一，有很多数学函数本身就是递归定义的，如阶乘函数当 n = 1 时，n!=1时，n!=1,当 n>1时，n!=nx(n-1)!;

其二，有些数据结构，如二叉树、广义表等，由于结构本身固有的递归特性，有关它们的操作，就可以采用递归函数来实现；

其三，还有一类问题，虽问题本身没有明显的递归结构，但用递归法求解，则更简洁明了，如快速排序问题、图的深度优先搜索问题等。