阅读本文需要的背景知识点：感知器学习算法、一丢丢编程知识

一、引言

  前面一节我们学习了机器学习算法系列（一）- 感知器学习算法（PLA），该算法可以将数据集完美的分成两种类型，但有一个前提条件就是假定数据集是线性可分的。

  在实际收集数据的过程中，可能因为各种各样的原因（例如反垃圾邮件的例子中收集的邮件单词错误或者是人工分类错误，将不是垃圾邮件的误认为是垃圾邮件）使得数据集中存在错误数据，这时数据集就可能不是线性可分的，感知器学习算法是没有办法停下来的，所以人们又基于感知器学习算法设计了一个可以处理线性不可分的算法——口袋算法（Pocket Algorithm）

二、模型介绍

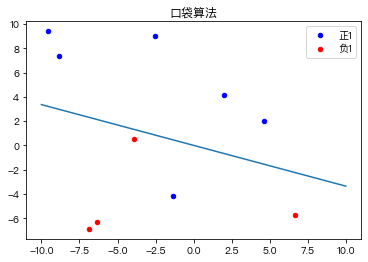
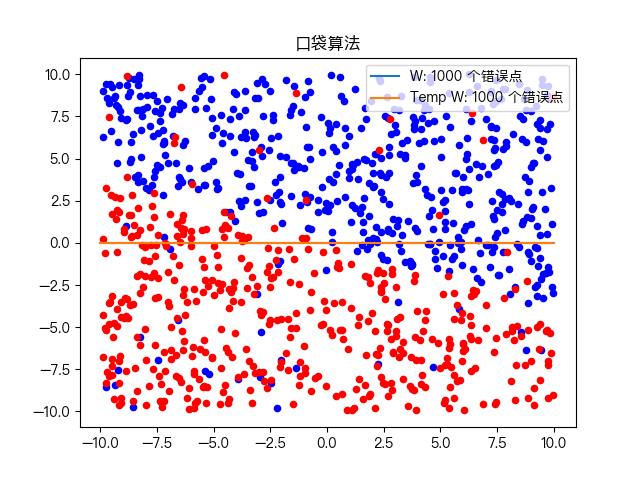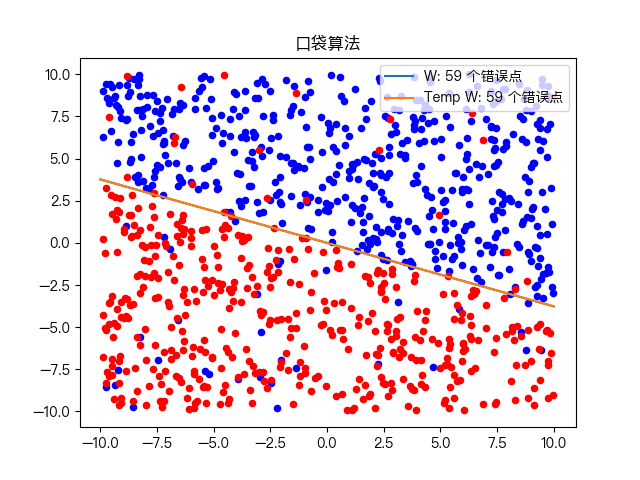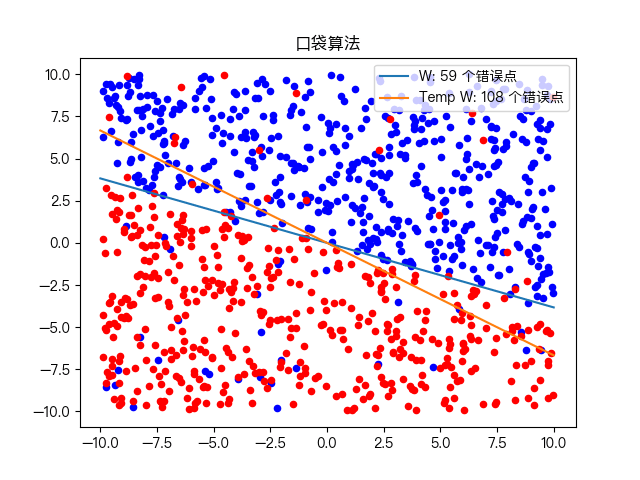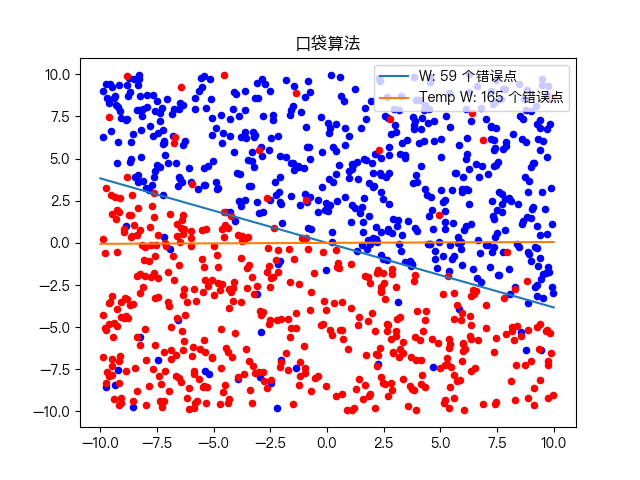
  口袋算法（Pocket Algorithm）是一个二元分类算法，将一个数据集通过线性组合的方式分成两种类型。如下图所示

  该算法是在感知器学习算法的基础上做的改进，其核心思想与感知器学习算法的思想一致，也是以错误为驱动，如果当前结果比口袋中的结果好，则将口袋中的结果替换为当前结果，口袋中保持着当前看到最好的结果，最后找到一个相对不错的答案，因此被命名为口袋算法。

三、算法步骤

初始化向量 w，例如 w 初始化为零向量
循环 t = 0，1，2 …
  找到一个随机的错误数据，即 h(x) 与目标值 y 不符
  $$\mathrm{sign}\left(w_t^T{x}_{n(t)}\right)\ne y_{n(t)}$$
  尝试修正向量 w，如果更新后的 w 的错误点相对更新前的 w 更少的时，则更新 w，反之进入下一次循环。
  $$w_{t+1}\leftarrow w_t+y_{n(t)}{x}_{n(t)}$$
直到到达设定的最大循环数时退出循环，所得的 w 即为一组方程的解

  由上面的步骤可以看到，由于不知道什么时候循环应该停下来，所以需要人为定义一个最大的循环次数来作为退出条件，所以口袋算法相对感知器学习算法来说，运行时间会更慢一些。在循环中是随机选取错误点，最后的输出结果在每次运行时也不是一个稳定的结果。

四、代码实现

使用 Python 实现口袋算法：

import numpy as np

def errorIndexes(w, X, y):
    """
    获取错误点的下标集合
    args:
        w - 权重系数
        X - 训练数据集
        y - 目标标签值
    return:
        errorIndexes - 错误点的下标集合
    """
    errorIndexes = []
    # 遍历训练数据集
    for index in range(len(X)):
        x = X[index]
        # 判定是否与目标值不符
        if x.dot(w) * y[index] <= 0:
            errorIndexes.append(index)
    return errorIndexes

def pocket(X, y, iteration, maxIterNoChange = 10):
    """
    口袋算法实现
    args:
        X - 训练数据集
        y - 目标标签值
        iteration - 最大迭代次数
        maxIterNoChange - 在提前停止之前没有提升的迭代次数
    return:
        w - 权重系数
    """
    np.random.seed(42)
    # 初始化权重系数
    w = np.zeros(X.shape[1])
    # 获取错误点的下标集合
    errors = errorIndexes(w, X, y)
    iterNoChange = 0
    # 循环
    for i in range(iteration):
        iterNoChange = iterNoChange + 1
        # 随机获取错误点下标
        errorIndex = np.random.randint(0, len(errors))
        # 计算临时权重系数
        tmpw = w + y[errors[errorIndex]] * X[errorIndex]
        # 获取临时权重系数下错误点的下标集合
        tmpErrors = errorIndexes(tmpw, X, y)
        # 如果错误点数量更少，就更新权重系数
        if len(errors) >= len(tmpErrors):
            iterNoChange = 0
            # 修正权重系数
            w = tmpw
            errors = tmpErrors
        # 提前停止
        if iterNoChange >= maxIterNoChange:
            break
    return w

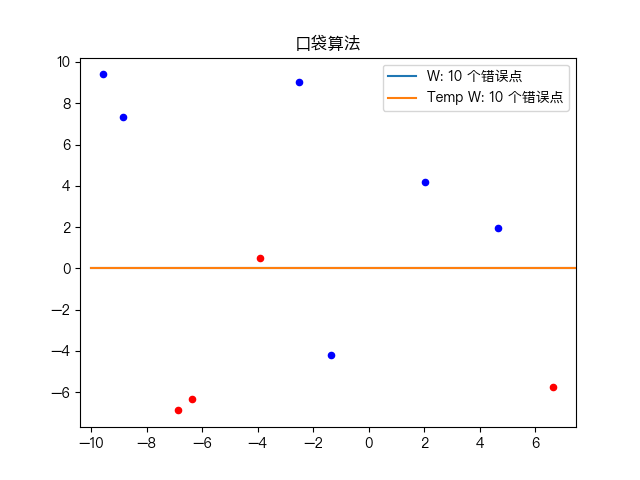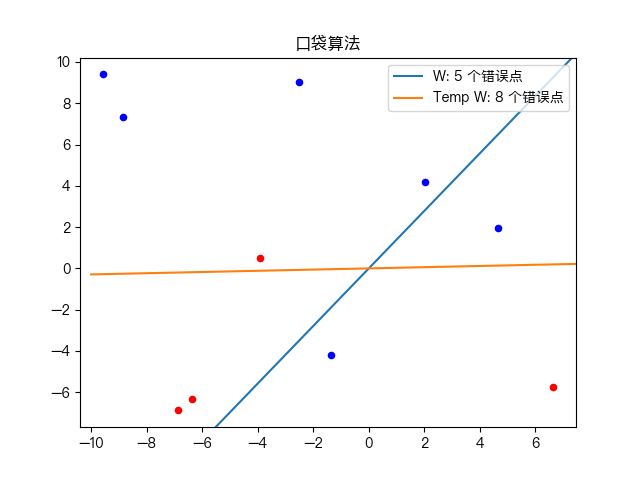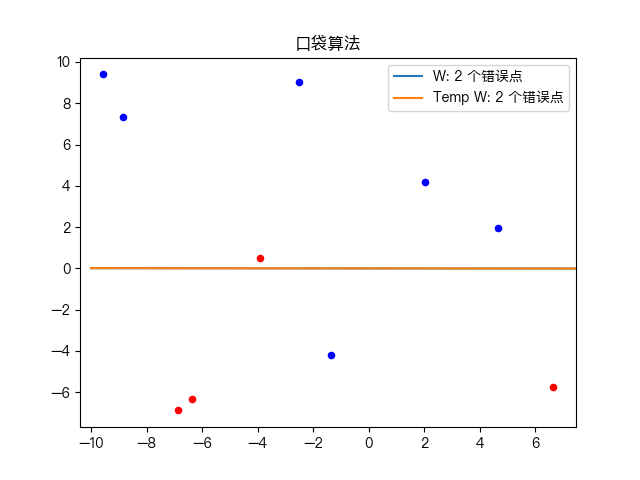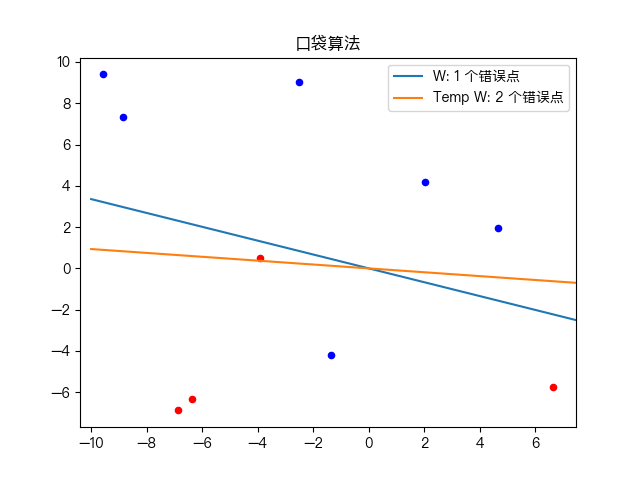
五、动画演示

简单训练数据集分类：

复杂训练数据集分类：

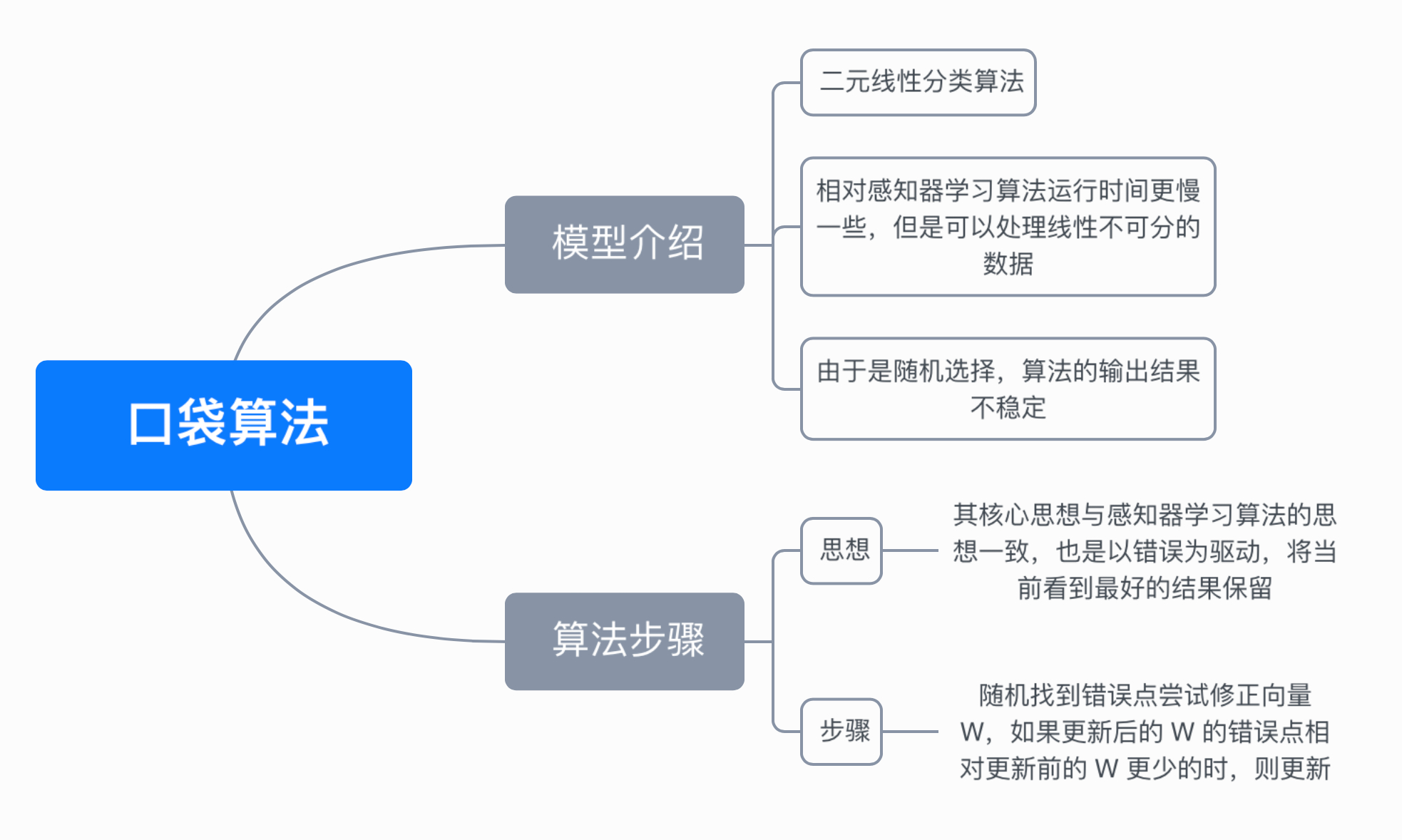
六、思维导图

完整演示请点击这里

注：本文力求准确并通俗易懂，但由于笔者也是初学者，水平有限，如文中存在错误或遗漏之处，恳请读者通过留言的方式批评指正