GitHub源码分享

主页地址：/gozhuyinglong.github.io
源码分享：github.com/gozhuyinglong/blog-demos

1. AVL树

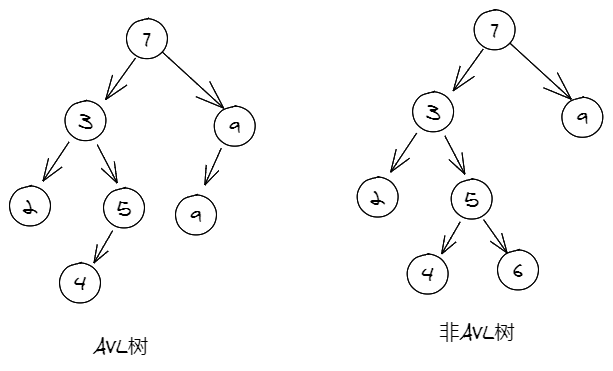
AVL（Adelson-Velskii 和 Landis）树是带有平衡条件的[二叉查找树]，又叫做平衡二叉树。在AVL树中任何节点的两个子树高度差最多为1，所以它又被称为高度平衡树。

如下图中可以清晰的看出，左边的树其根节点左子树高度为3，右子树高度为2，符合AVL树的特点；而右边的树其根节点左子树高度为3，右子树高度为1，不符合AVL树的特点。因此左边的树为AVL树，右边的树不是AVL树。

那么怎样才能保持这种平衡呢？

答案便是在插入或删除节点时，通过对树进行简单的修正来保持平衡，我们称之为旋转。

2. 旋转（rotation）

旋转分为单旋转（single rotation）和双旋转（double rotation）。

• 当左右子树的高度差超过1，并且最高的叶子节点在“外边”时，使用单旋转。
• 当左右子树的高度差超过1，并且最高的叶子节点在“里面”时，使用双旋转。

而单旋转又分为：

• 左旋转，即向左旋转。当右子树的高度大于左子树时，进行左旋转。
• 右旋转，即向右旋转。当左子树的高度大于右子树时，进行右旋转。

双旋转又分为：

• 左-右双旋转，即先向左旋转（左子节点），再向右旋转。当左子树的高度大小右子树，并且左子树最高的叶子节点为其父节点的右子节点，那么需要左-右双旋转。
• 右-左双旋转，即先向右旋转（右子节点），再向左旋转。当右子树的高度大小左子树，并且右子树最高的叶子节点为其父节点的左子节点，那么需要右-左双旋转。

单看这些名词概念是不容易理解的，下面我们通过图例来逐个介绍。

3. 左旋转

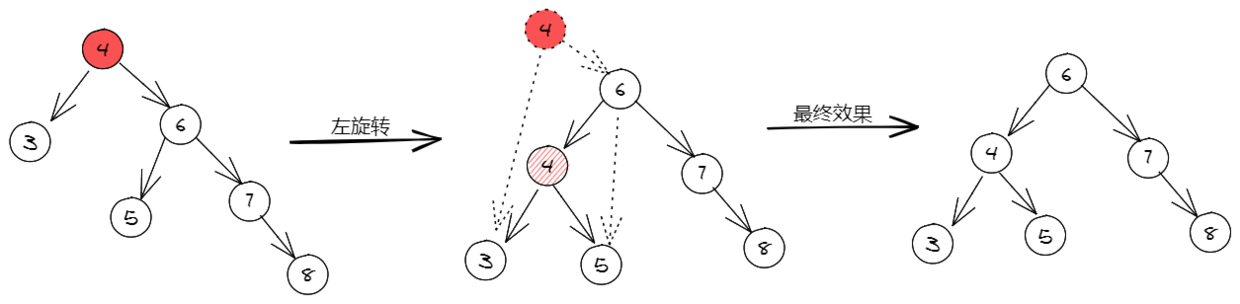
看下图中左边的树，该树是一棵二叉查找树，但是否满足AVL的特性呢？可以发现其根节点的左子树的高度为1，而右子树的高度为3，所以其不一棵AVL树。

经过观察，其右子树高于左子树，并且最高的叶子节点也在右边，那么我们使用左旋转进行平衡。

详细旋转过程：

• 将根节点4复制出一个新的节点，其左子节点为3保持不变，将其右子节点指向5（即原根节点的右子节点的左子节点）。
• 将原根节点的右子节点6的左子节点指向新节点4，其右子节点为7保持不变，那么6便成了新的根节点。

哈哈，是不是有点绕，其实也可以简单理解为：既然右子树比左子树高，那么将树根4向左下移，将树根的右子节点6向上移，成为新的树根，这样便使左右子树的高度平衡了。结合上图，反复练习几次吧。

4. 右旋转

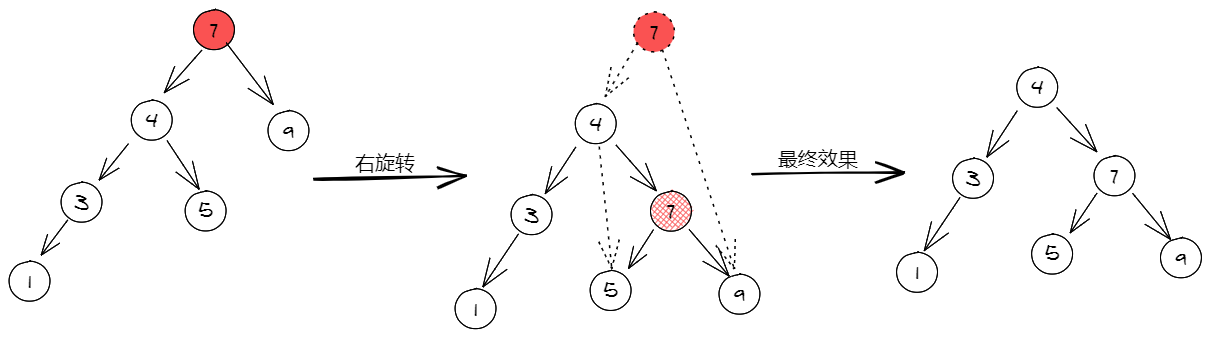
右旋转与左旋转正好是对称的，看下图中左边的树，该二叉查找树的左子树高度为3，而右子树高度为1，不满足AVL树的旋转。

因其左子树高于右子树，并且最高的叶子节点在左边，所以我们使用右旋转。

详细旋转过程：

• 将根节点7复制出一个新的节点，其右子节点为9保持不变，左子节点指向5（即原根节点的左子节点的右子节点）。
• 将原根节点的左节点升级为新的根节点，即其左子树为3保持不变，右子节点指向新的根节点7。

左旋转与右旋转一定要理解，不然下面的双旋转就更容易晕菜了！

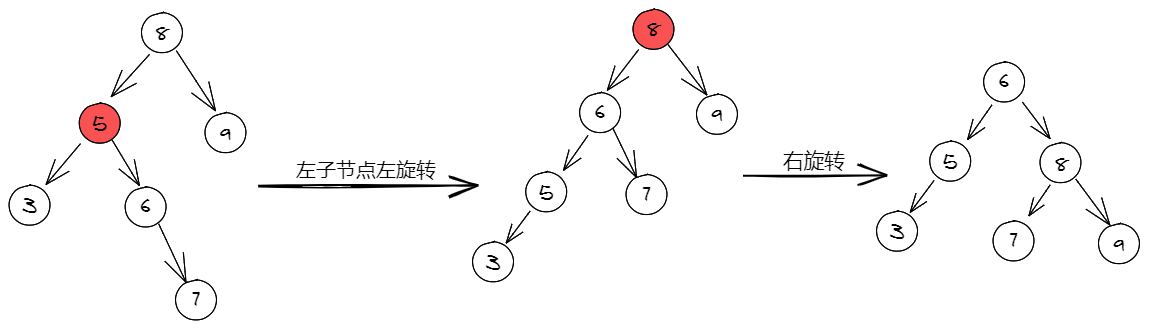
5. 双旋转

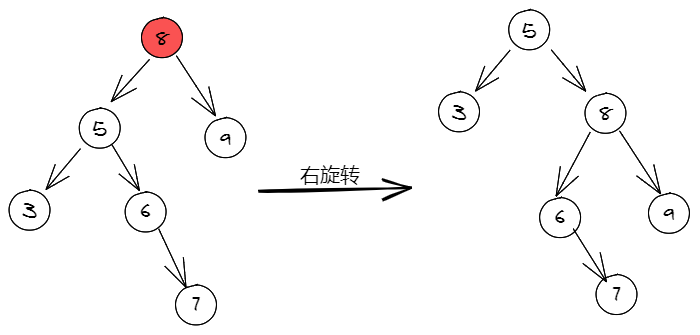
在介绍双旋转之前，先来看下图，其根节点的左子树高度为3，右子树高度为9，那么我们先使用右旋转的方式，看能不能达平衡的效果。

通过观察右旋转后的效果，是不满足AVL树的特性的。这便需要使用双旋转了。

我们使用左-右旋转来平衡上图中的树，即先进行左旋转，再进行右旋转，但其平衡点不同，如下图所示。

详细旋转过程：

• 先将根节点的左子树（5节点）进行左旋转，降低其（5节点）右子树的高度。
• 再将根节点进行右旋转，便达到了平衡效果。

那么反过来，右-左双旋转的详细过程：

• 先将根节点的右子树进行右旋转，降低其右子树的高度。
• 再将根节点进行左旋转。

6. 代码实现

AVL树的实现是在[二叉查找树]的基础上添加了平衡操作。

6.1 求节点高度

在Node类中添加节点高度方法height、leftHeight和rightHeight，若节点为空则高度为0。

// 当前节点高度
public int height() {
    return Math.max(left == null ? 0 : left.height(), right == null ? 0 : right.height()) + 1;
}

// 左子节点高度
public int leftHeight() {
    if (left == null) {
        return 0;
    }
    return left.height();
}

// 右子节点高度
public int rightHeight() {
    if (right == null) {
        return 0;
    }
    return right.height();
}

6.2 左旋转

在Node类中增加左旋转方法leftRotate。

public void leftRotate() {
    // 将当前节点向左下移，成为新的左节点
    Node newLeftNode = new Node(element);
    newLeftNode.left = left;
    // 将右子节点设为原根节点右子树的左子树
    newLeftNode.right = right.left;

    // 将右节点上移，成为新的树根（当前节点）
    element = right.element;
    // 将左子节点设为新的左子节点（原树根）
    left = newLeftNode;
    right = right.right;
}

6.3 右旋转

在Node类中增加右旋转方法rightRotate。

public void rightRotate() {
    // 将当前节点向右下移，成为新的右子节点
    Node newRightNode = new Node(element);
    // 将左子节点指向原根节点的左子树的右子树
    newRightNode.left = left.right;
    newRightNode.right = right;

    // 将左子节点上移，成为新的树根（当前节点）
    element = left.element;
    left = left.left;
    // 将右子节点设为新的右子节点（原树根）
    right = newRightNode;
}

6.4 平衡方法

在AVLTree类中添加平衡方法balance，该方法用于判断是需要单旋转还是双旋转。

public void balance(Node node) {

    if (node == null) {
        return;
    }

    if (node.leftHeight() - node.rightHeight() > 1) {
        if (node.left.rightHeight() > node.left.leftHeight()) {
            node.left.leftRotate();
        }
        node.rightRotate();

    } else if (node.rightHeight() - node.leftHeight() > 1) {
        if (node.right.leftHeight() > node.right.rightHeight()) {
            node.right.rightHeight();
        }
        node.leftRotate();
    }
}

6.5 添加节点

在AVLTree类中增加添加节点方法，当添加完一个节点后，进行调用balance方法，来维持平衡。

private void add(Node node, int element) {
    if (node.compareTo(element) < 0) {
        if (node.left == null) {
            node.left = new Node(element);
        } else {
            add(node.left, element);
        }
    } else if (node.compareTo(element) > 0) {
        if (node.right == null) {
            node.right = new Node(element);
        } else {
            add(node.right, element);
        }
    }
    balance(node);
}

6.6 删除节点

在AVLTree类中增加删除节点方法，当删除完一个节点后，也进行调用balance方法，来维护平衡。

private void remove(Node parentNode, Node node, int element) {
    if (node == null) {
        return;
    }
    // 先找到目标元素
    int compareResult = node.compareTo(element);
    if (compareResult < 0) {
        remove(node, node.left, element);
    } else if (compareResult > 0) {
        remove(node, node.right, element);
    } else {
        // 找到目标元素，判断该节点是父节点的左子树还是右子树
        boolean isLeftOfParent = false;
        if (parentNode.left != null && parentNode.left.compareTo(element) == 0) {
            isLeftOfParent = true;
        }

        // 删除目标元素
        if (node.left == null && node.right == null) { // （1）目标元素为叶子节点，直接删除
            if (isLeftOfParent) {
                parentNode.left = null;
            } else {
                parentNode.right = null;
            }
        } else if (node.left != null && node.right != null) { // （2）目标元素即有左子树，也有右子树
            // 找到右子树最小值（叶子节点），并将其删除
            Node minNode = findMin(node.right);
            remove(minNode.element);
            // 将该最小值替换要删除的目标节点
            minNode.left = node.left;
            minNode.right = node.right;
            if (isLeftOfParent) {
                parentNode.left = minNode;
            } else {
                parentNode.right = minNode;
            }

        } else { // （3）目标元素只有左子树，或只有右子树
            if (isLeftOfParent) {
                parentNode.left = node.left != null ? node.left : node.right;
            } else {
                parentNode.right = node.left != null ? node.left : node.right;
            }
        }
    }
    balance(node);
}

6.7 完整代码

由于完整代码篇幅过长，这里就不展示了，可以通过GitHub进行访问，地址如下：
github.com/gozhuyinglong/blog-demos/blob/main/java-data-structures/src/main/java/io/github/gozhuyinglong/datastructures/tree/AVLTreeDemo.java

7. 总结

总结一句话来表示AVL树：AVL树是一棵其平衡因子（左右子树的高度差）的绝对值小于1的二叉查找树，其可以通过单旋转或双旋转来保持平衡。